题目内容
4．如图，把一个矩形的纸片按图示对折两次，然后剪下一部分，为了得到一个钝角为110°的菱形，剪口与第二次折痕所成角的度数应为（ ）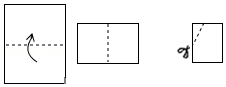
| A． | 70°或20° | B． | 55°或45° | C． | 55°或35° | D． | 55°或65° |
分析 折痕为AC与BD，∠BAD=110°，根据菱形的性质：菱形的对角线平分对角，可得∠ABD=35°，易得∠BAC=55°，所以剪口与折痕所成的角a的度数应为35°或55°．
解答 解：∵四边形ABCD是菱形，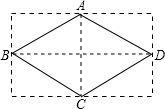
∴∠ABD=$\frac{1}{2}$∠ABC，∠BAC=$\frac{1}{2}$∠BAD，AD∥BC，
∵∠BAD=110°，
∴∠ABC=180°-∠BAD=180°-110°=70°，
∴∠ABD=30°，∠BAC=55°．
∴剪口与折痕所成的角a的度数应为35°或55°．
故选：C．
点评 此题主要考查菱形的判定以及折叠问题，关键是熟练掌握菱形的性质：菱形的对角线平分每一组对角．
练习册系列答案
相关题目
19．a，b，c为△ABC的三边，化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|，结果是（ ）
| A． | 0 | B． | 2a+2b+2c | C． | 4a | D． | 2b-2c |
如图，在△ABC中，∠B＞∠C，AD⊥BC，垂足为D，AE平分∠BAC． 
如图，正方形ABCD，AC、BD交于点O，点E、F分别在AB、BC上，且∠EOF=90°，则下列结论①AE=BF，②OE=OF，③BE+BF=AD，④AE2+CF2=2OE2中正确的有①②③④（只写序号）
19．
有这样一个问题：探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质．
小东根据学习函数的经验，对函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质进行了探究．
下面是小东的探究过程，请补充完整：
（1）函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值，求m的值；
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）进一步探究发现，该函数图象在第三象限内的最高点的坐标是（-2，-$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）当x＞0时，y随x的增大而增大．
有这样一个问题：探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质．小东根据学习函数的经验，对函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质进行了探究．
下面是小东的探究过程，请补充完整：
（1）函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值，求m的值；
| x | … | -4 | -3 | -2 | -$\frac{3}{2}$ | -1 | -$\frac{2}{3}$ | $\frac{2}{3}$ | 1 | 2 | 3 | 4 | … |
| y | … | -$\frac{17}{8}$ | -$\frac{31}{18}$ | -$\frac{3}{2}$ | -$\frac{59}{36}$ | -$\frac{5}{2}$ | -$\frac{29}{6}$ | -$\frac{25}{6}$ | -$\frac{3}{2}$ | $\frac{1}{2}$ | $\frac{23}{18}$ | m | … |
（4）进一步探究发现，该函数图象在第三象限内的最高点的坐标是（-2，-$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）当x＞0时，y随x的增大而增大．