题目内容
5.已知二次函数y=m (x-1)( x-4)的图象与x轴交于A、B两点(点A在点B的左边),顶点为C,将该二次函数的图象关于x轴翻折,所得图象的顶点为D.若四边形ACBD为正方形,则m的值为±$\frac{2}{3}$.分析 根据已知条件得到A(1,0),B(4,0),得到抛物线的对称轴为直线x=$\frac{1+4}{2}$=$\frac{5}{2}$,设顶点C的坐标为($\frac{5}{2}$,a),根据已知条件列方程即可得到结论.
解答 解:∵二次函数y=m (x-1)( x-4)的图象与x轴交于A、B两点,
∴A(1,0),B(4,0),
∴抛物线的对称轴为直线x=$\frac{1+4}{2}$=$\frac{5}{2}$,
设顶点C的坐标为($\frac{5}{2}$,a),
∵四边形ACBD为正方形,
∴|a|=$\frac{3}{2}$,
∴C($\frac{5}{2}$,$\frac{3}{2}$)或C($\frac{5}{2}$,-$\frac{3}{2}$),
把C点的坐标代入得,$\frac{3}{2}$=m($\frac{5}{2}$-1)( $\frac{5}{2}$-4)或-$\frac{3}{2}$=m($\frac{5}{2}$-1)( $\frac{5}{2}$-4),
解得:m=$±\frac{2}{3}$,
故答案为:±$\frac{2}{3}$.
点评 本题考查了抛物线与x轴的交点问题,二次函数的图象与几何变换,正方形的性质,正确的理解题意是解题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
15.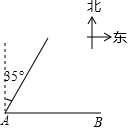 如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )
如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )
 如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )
如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )| A. | 北偏东55° | B. | 北偏西55° | C. | 北偏东35° | D. | 北偏西35° |
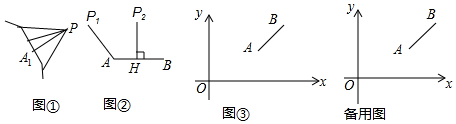
 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发3h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
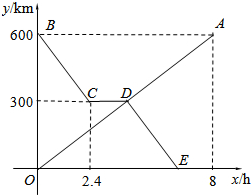
货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发3h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.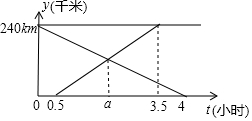 甲、乙两车分别从A、B两地相向而行,甲车出发0.5小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是两车离B地距离y与甲车出发时间t(小时)之间的函数图象.
甲、乙两车分别从A、B两地相向而行,甲车出发0.5小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是两车离B地距离y与甲车出发时间t(小时)之间的函数图象.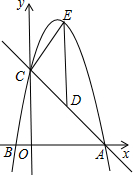 如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A(5,0),B(-1,0),点D在直线AC上,过点D作DE∥y轴交抛物线于点E,设点D的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A(5,0),B(-1,0),点D在直线AC上,过点D作DE∥y轴交抛物线于点E,设点D的横坐标为m.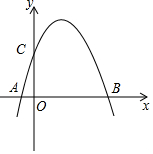 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点,O为坐标原点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点,O为坐标原点.