题目内容
20.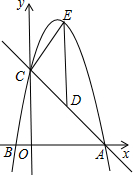 如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A(5,0),B(-1,0),点D在直线AC上,过点D作DE∥y轴交抛物线于点E,设点D的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A(5,0),B(-1,0),点D在直线AC上,过点D作DE∥y轴交抛物线于点E,设点D的横坐标为m.(1)求抛物线和直线AC的解析式;
(2)当0<m<5时,用含m的代数式表示DE的长;
(3)在(2)的条件下,当m为何值时,△CDE是轴对称图形?
分析 (1)将A、B点代入抛物线解析式即可求得b、c的值,即可求得点C坐标,即可解题;
(2)延长ED交x轴于点F,易证△ADF为等腰直角三角形,根据DE=EF-DF即可解题;
(3)作DG⊥y轴,易证△CDE是等腰直角三角形,根据(2)中结论即可求得m的值,即可解题.
解答 解:(1)将A、B代入y=-x2+bx+c可得:$\left\{\begin{array}{l}{0=-1-b+c}\\{0=-25+5b+c}\end{array}\right.$,
解得:b=4,c=5,
∴抛物线解析式为y=-x2+4x+5,
∴点C坐标为(0,5),
设直线AC解析式为y=kx+b,代入A、C得:$\left\{\begin{array}{l}{b=5}\\{5k+b=0}\end{array}\right.$,
解得:k=-1,b=5,
∴直线AC的解析式为y=-x+5;
(2)延长ED交x轴于点F,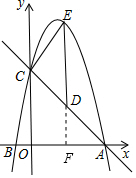
∵OA=OC,
∴∠BAC=45°,
∵ED∥y轴,
∴△ADF为等腰直角三角形,
∴DF=AF,
∴DE=EF-DF=(-m2+4m+5)-(5-m)=-m2+5m;
(3)作DG⊥y轴,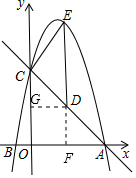
∴∠ACO=45°,
∴CD=$\sqrt{2}$DG,
∵△CDE是轴对称图形,∠CDE=∠ADF=45°,
∴△CDE是等腰直角三角形,
∴DE=$\sqrt{2}$CD,
∴DE=2DG,即-m2+5m=2m,
解得:m=3或m=0(舍去),
∴当m=3时,△CDE是轴对称图形.
点评 本题考查了代入法求二次函数解析式的方法,考查了等腰直角三角形的性质,本题中求得DE的长与m的关系是解题的关键.

练习册系列答案
相关题目
10.下列事件中,是确定事件的是( )
| A. | 三条线段围成一个三角形 | B. | 1小时等于60分钟 | ||
| C. | 度量三角形的内角和结果为360° | D. | 数轴上一点表示有理数 |
 某校七年级某班期末测试全班所有学生数学成绩的频数分布直方图如图所示(满分100分),则该班成绩在85.5~95.5这一分数段的学生数是30.
某校七年级某班期末测试全班所有学生数学成绩的频数分布直方图如图所示(满分100分),则该班成绩在85.5~95.5这一分数段的学生数是30.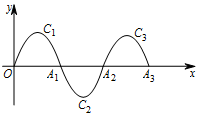 如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )
如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )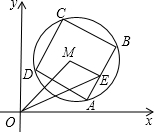 如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.
如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.