题目内容
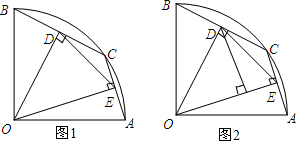
如图1,在半径为2的扇形AOB中,∠AOB=90°,点C是
上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为点D、点E.
(1)当BC=1时,求线段OD的长;
(2)在点C的运动过程中,△DOE中是否存在长度保持不变的边或度数保持不变的角?如果存在,请指出并求其长度或度数(只求一种即可);如果不存在,请说明理由;
(3)作DF⊥OE于点F(如图2),当DF2+EF取得最大值时,求sin∠BOD的值.
 |
| AB |
(1)当BC=1时,求线段OD的长;
(2)在点C的运动过程中,△DOE中是否存在长度保持不变的边或度数保持不变的角?如果存在,请指出并求其长度或度数(只求一种即可);如果不存在,请说明理由;
(3)作DF⊥OE于点F(如图2),当DF2+EF取得最大值时,求sin∠BOD的值.

考点:圆的综合题
专题:
分析:(1)根据垂径定理,可得BD的长度,根据勾股定理,可得答案;
(2)根据勾股定理,可得AB的长度,根据三角形的中位线,可得答案,根据垂径定理,可得圆心角相等,根据角的和差,可得答案;
(3)根据勾股定理,可得DF2,根据二次函数的最值,可得DF的长度,根据等腰直角三角形的性质,可得OD的长度,根据正弦的含义,可得答案.
(2)根据勾股定理,可得AB的长度,根据三角形的中位线,可得答案,根据垂径定理,可得圆心角相等,根据角的和差,可得答案;
(3)根据勾股定理,可得DF2,根据二次函数的最值,可得DF的长度,根据等腰直角三角形的性质,可得OD的长度,根据正弦的含义,可得答案.
解答:解:(1)∵点O是圆心,OD⊥BC,BC=1,
∴BD=
BC=
.
又∵OB=2,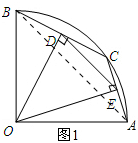
∴OD=
=
=
;
(2)存在,DE的长度是不变的.
如图1,连结AB,
则AB=
=2
,
∵点D、点E分别是BC、AC的中点,
∴DE=
AB=
.
存在,∠DOE的度数是不变的.
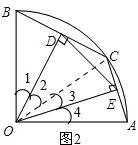
如图2,连结OC,
可得∠1=∠2,∠3=∠4,
∵∠AOB=90°
∴∠2+∠3=45°即∠DOE=45°;
(3)如图3,设EF=x,由(2)可知DE=
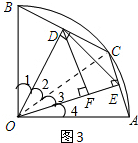
在Rt△DFE中,DF2=DE2-EF2=2-x2
∴DF 2+EF=-x2+x+2
∴当x=
,即EF=
时,DF 2+EF取得最大值,
此时,DF=
由(2)可知∠DOE=45°,
∴△DOF是等腰直角三角形,
∴OD=
在Rt△BOD中,BD=
=
=
∴sin∠BOD=
=
=
.
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
又∵OB=2,

∴OD=
| OB2-BD2 |
22-(
|
| ||
| 2 |
(2)存在,DE的长度是不变的.
如图1,连结AB,
则AB=
| OB2+OA2 |
| 2 |
∵点D、点E分别是BC、AC的中点,
∴DE=
| 1 |
| 2 |
| 2 |

存在,∠DOE的度数是不变的.
如图2,连结OC,
可得∠1=∠2,∠3=∠4,
∵∠AOB=90°
∴∠2+∠3=45°即∠DOE=45°;
(3)如图3,设EF=x,由(2)可知DE=
| 2 |

在Rt△DFE中,DF2=DE2-EF2=2-x2
∴DF 2+EF=-x2+x+2
∴当x=
| 1 |
| 2 |
| 1 |
| 2 |
此时,DF=
| ||
| 2 |
由(2)可知∠DOE=45°,
∴△DOF是等腰直角三角形,
∴OD=
| ||
| 2 |
在Rt△BOD中,BD=
| OB2-OD2 |
22-(
|
| ||
| 2 |
∴sin∠BOD=
| BD |
| OB |
| ||||
| 2 |
| ||
| 4 |
点评:本题考查了圆的综合题,熟练应用利用垂径定理,勾股定理,三角形的中位线的性质是解题关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
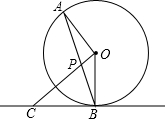 如图,AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC.
如图,AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC.