题目内容
19.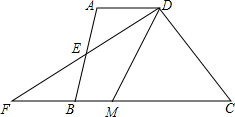 如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点M在BC边上,且∠MDF=∠ADF.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点M在BC边上,且∠MDF=∠ADF.(1)求证:△ADE≌△BFE.
(2)连接EM,如果FM=DM,判断EM与DF的关系,并说明理由.
分析 (1)由平行线的性质得出∠ADE=∠BFE,由E为AB的中点,得出AE=BE,由AAS证明△AED≌△BFE即可;
(2)由△AED≌△BFE,得出对应边相等DE=EF,证明FM=DM,由三角形的三线合一性质得出EM⊥DF,即可得出结论.
解答 (1)证明:∵AD∥BC,
∴∠ADE=∠BFE,
∵E为AB的中点,
∴AE=BE,
在△AED和△BFE中,$\left\{\begin{array}{l}{∠ADE=∠BFE}&{\;}\\{AE=BE}&{\;}\\{∠AED=∠BEF}&{\;}\end{array}\right.$,
∴△AED≌△BFE(AAS);
(2)解:EM与DM的关系是EM垂直且平分DF;理由如下: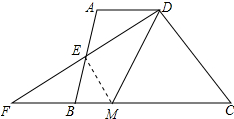
连接EM,如图所示:
由(1)得:△AED≌△BFE,
∴DE=EF,
∵∠MDF=∠ADF,∠ADE=∠BFE,
∴∠MDF=∠BFE,
∴FM=DM,
∴EM⊥DF,
∴ME垂直平分DF.
点评 本题考查了平行线的性质、全等三角形的判定与性质、等腰三角形的判定与性质;熟练掌握全等三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
10.如果等腰直角三角形的两边长为2cm,4cm,那么它的周长为( )
| A. | 8cm | B. | 10cm | C. | 11cm | D. | 8cm或10cm |
14.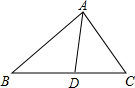 如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
 如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )| A. | 3:4 | B. | 4:3 | C. | 16:9 | D. | 9:16 |
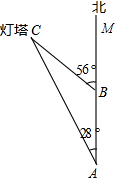 如图,14:00时,一条船从A处出发,以18海里/小时的速度,向正北航行,16:00时,船到达B处,从A处测得灯塔C在北偏西28°,从B处测得灯塔C在北偏西56°,求B处到灯塔C的距离.
如图,14:00时,一条船从A处出发,以18海里/小时的速度,向正北航行,16:00时,船到达B处,从A处测得灯塔C在北偏西28°,从B处测得灯塔C在北偏西56°,求B处到灯塔C的距离. 如图,AB是⊙O的直径,C是⊙O上的一点,AD垂直于过点C的切线,垂足为D,∠BAD=70°,则∠DAC=35°.
如图,AB是⊙O的直径,C是⊙O上的一点,AD垂直于过点C的切线,垂足为D,∠BAD=70°,则∠DAC=35°.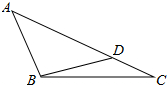 已知:如图,在△ABC中,AC=9,BC=6,请问,在边AC上是否存在一点D,使△ABC∽△BDC?若存在请求出CD的长,若不存在,请说明理由.
已知:如图,在△ABC中,AC=9,BC=6,请问,在边AC上是否存在一点D,使△ABC∽△BDC?若存在请求出CD的长,若不存在,请说明理由.