题目内容
14．
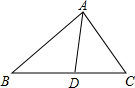如图，在△ABC中，AD是它的角平分线，AB=8cm，AC=6cm，则S△ABD：S△ACD=（ ）| A． | 3：4 | B． | 4：3 | C． | 16：9 | D． | 9：16 |
分析 利用角平分线的性质，可得出△ABD的边AB上的高与△ACD的AC上的高相等，估计三角形的面积公式，即可得出△ABD与△ACD的面积之比等于对应边之比．
解答 解：∵AD是△ABC的角平分线，
∴设△ABD的边AB上的高与△ACD的AC上的高分别为h1，h2，
∴h1=h2，
∴△ABD与△ACD的面积之比=AB：AC=8：6=4：3，
故选：B．
点评 本题考查了角平分线的性质，以及三角形的面积公式，熟练掌握三角形角平分线的性质是解题的关键．
练习册系列答案
相关题目
4．地球村的粮食产量每年增长10%，如果去年的粮食产量为a千克，那么明年的粮食产量为（ ）千克．
| A． | （1+10%）a | B． | （1+10%）a2 | C． | 10%a | D． | （1+10%）a3 |
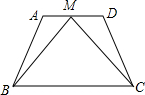已知：如图，AB=CD，∠A=∠D，点M是AD的中点．
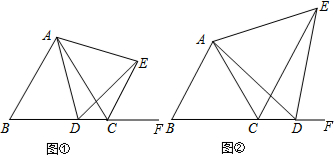
如图，△ABC中，AB=AC，BD=CE，BE=CF，若∠A=50°，则∠DEF的度数是65°．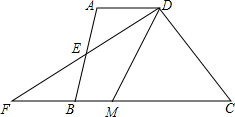
如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点M在BC边上，且∠MDF=∠ADF．
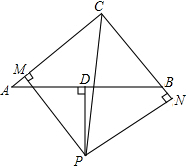如图，在△ABC中，D是AB边的中点，PD⊥AB交∠ACB的平分线与点P，PM⊥AC于点M，PN⊥BC交CB的延长线于点N．
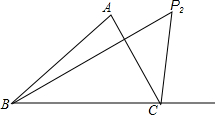如图，分别在△ABC的一个内角∠ABC和一个外角∠ACD内部作射线BP2、CP2相交于点P2，∠P2BC=3∠ABP2，∠P2CD=3∠ACP2，直接写出∠A、∠P2之间满足的数量关系．