题目内容
4.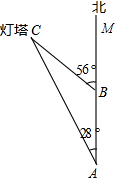 如图,14:00时,一条船从A处出发,以18海里/小时的速度,向正北航行,16:00时,船到达B处,从A处测得灯塔C在北偏西28°,从B处测得灯塔C在北偏西56°,求B处到灯塔C的距离.
如图,14:00时,一条船从A处出发,以18海里/小时的速度,向正北航行,16:00时,船到达B处,从A处测得灯塔C在北偏西28°,从B处测得灯塔C在北偏西56°,求B处到灯塔C的距离.
分析 根据所给的角的度数,容易证得△BCA是等腰三角形,而AB的长易求,所以根据等腰三角形的性质,BC的值也可以求出.
解答 解:据题意得,∠A=28°,∠DBC=56°,
∵∠DBC=∠A+∠C,
∴∠A=∠C=28°,
∴AB=BC,
∵AB=18×2=36,
∴BC=36(海里).
∴B处到灯塔C的距离36(海里).
点评 本题考查了等腰三角形的性质及方向角的问题;由已知得到三角形是等腰三角形是正确解答本题的关键.要学会把实际问题转化为数学问题,用数学知识进行解决实际问题的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
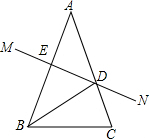 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AC于点D,交AB于E.
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AC于点D,交AB于E.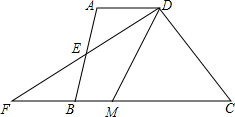 如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点M在BC边上,且∠MDF=∠ADF.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点M在BC边上,且∠MDF=∠ADF.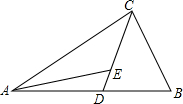 如图,△ABC中,点D在AB边上,AD=CD,点E在CD上,∠ABC+∠AEC=180°,图中是否存在与BC相等的线段?若存在,请找出,并加以证明,若不存在,请说明理由.
如图,△ABC中,点D在AB边上,AD=CD,点E在CD上,∠ABC+∠AEC=180°,图中是否存在与BC相等的线段?若存在,请找出,并加以证明,若不存在,请说明理由.