题目内容
11.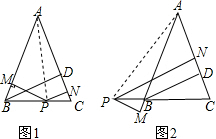 如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN.
如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN.如图2,当点P在CB的延长线上,且上面问题中其他条件不变时的图形,他猜想此时BD,PM,PN之间的数量关系并证明你的结论.
分析 (1)利用等积法,由条件可得S△ABC=S△ABP+S△APC,利用三角形的面积公式,结合AB=AC可证得结论;
(2)同(1)利用等积法可得S△ABC=S△APC-S△PAB,则可得到BD=PN-PM.
解答 (1)证明:
∵BD是△ABC的高,PM⊥AB,PN⊥AC,
∴S△ABC=$\frac{1}{2}$AC•BD,S△ABP=$\frac{1}{2}$AB•PM,S△APC=$\frac{1}{2}$AC•PN,
∵S△ABC=S△ABP+S△APC,
∴$\frac{1}{2}$AC•BD=$\frac{1}{2}$AB•PM+$\frac{1}{2}$AC•PN,
∵AB=AC,
∴BD=PM+PN;
(2)解:BD=PN-PM,
证明如下:
∵BD是△ABC的高,PM⊥AB,PN⊥AC,
∴S△ABC=$\frac{1}{2}$AC•BD,S△ABP=$\frac{1}{2}$AB•PM,S△APC=$\frac{1}{2}$AC•PN,
∵S△ABC=S△APC-S△PAB
∴$\frac{1}{2}$AC•BD=$\frac{1}{2}$AC•PN-$\frac{1}{2}$AB•PM,
∵AB=AC,
∴BD=PN-PM.
点评 本题主要考查等积法的应用,所谓等积法即从不同的角度表示同一个图形的面积,从而得到所需要的关系式,灵活利用等积法可起到事半功倍的效果.

练习册系列答案
相关题目
1.如表,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
(1)可求得c=9,第2015个格子中的数为-5;
(2)如果x、y为前三个格子中的任意两个数,那么所有的|x-y|的和可以通过计算|9-a|+|a-9|+|9-b|+|b-9|+|a-b|+|b-a|得到,求所有的|x-y|的和;
(3)前m个格子中所填整数之和是否可能为2015?若能,求m的值;若不能,请说出理由.
| 9 | a | b | c | -5 | 1 | … |
(2)如果x、y为前三个格子中的任意两个数,那么所有的|x-y|的和可以通过计算|9-a|+|a-9|+|9-b|+|b-9|+|a-b|+|b-a|得到,求所有的|x-y|的和;
(3)前m个格子中所填整数之和是否可能为2015?若能,求m的值;若不能,请说出理由.
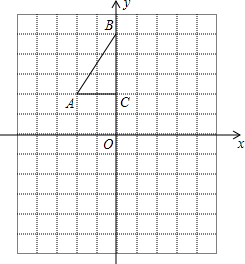 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).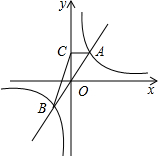 如图,正比例函数y1=mx(m>0)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于点A(n,4)和点B,AC⊥y轴,垂足为M,△ACB的面积为8.
如图,正比例函数y1=mx(m>0)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于点A(n,4)和点B,AC⊥y轴,垂足为M,△ACB的面积为8.