题目内容
4.在平行四边形ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是( )| A. | 2<AD<18 | B. | 1≤AD≤9 | C. | 2≤AD≤8 | D. | 1<AD<9 |
分析 根据平行四边形的性质求出OA和OD,在△AOD中,根据三角形三边关系定理得出5-4<AD<5+4,求出即可.
解答  解:∵四边形ABCD是平行四边形,AC=10,BD=8,
解:∵四边形ABCD是平行四边形,AC=10,BD=8,
∴OA=OC=5,OB=OD=4,
在△AOD中,由三角形三边关系定理得:5-4<AD<5+4,
即1<AD<9,
故选:D.
点评 本题考查了三角形的三边关系定理和平行四边形的性质,注意:平行四边形的对角线互相平分.

练习册系列答案
相关题目
15.下列有关相反数的说法:①符号相反的数叫相反数;②数轴上原点两旁的数是相反数;③-(-3)的相反数是-3;④-a一定是负数;⑤)若两个数之和为0,则这两个数互为相反数; ⑥若两个数互为相数,则这两个数一定是一个正数一个负数.其中正确的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9. 如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠A=60°,则∠CDB的度数等于( )
如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠A=60°,则∠CDB的度数等于( )
 如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠A=60°,则∠CDB的度数等于( )
如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠A=60°,则∠CDB的度数等于( )| A. | 70° | B. | 100° | C. | 110° | D. | 120° |
13.若4a2+(k-1)a+9是一个关于a的完全平方式,则k的值为( )
| A. | 12 | B. | -11 | C. | 13 | D. | -11或13 |
14. 已知:如图,由AB∥DC,可以判断( )
已知:如图,由AB∥DC,可以判断( )
 已知:如图,由AB∥DC,可以判断( )
已知:如图,由AB∥DC,可以判断( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠2=∠3 | D. | ∠1=∠4 |
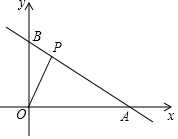 直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).
直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).