题目内容
如图，在五边形ABCDE中，AE∥BC，探索∠A+∠B与∠C+∠D+∠E的度数之间的数量关系，并说明理由．考点：平行线的性质
专题：
分析：首先过点D作DF∥AE，交AB于点F，由AE∥BC，可证得AE∥DF∥BC，然后由两直线平行，同旁内角互补，证得∠A+∠B=180°，∠E+∠EDF=180°，∠CDF+∠C=180°，继而证得结论．
解答：
解：∠C+∠D+∠E=2（∠A+∠B）．
理由：过点D作DF∥AE，交AB于点F，
∵AE∥BC，
∴AE∥DF∥BC，
∴∠A+∠B=180°，∠E+∠EDF=180°，∠CDF+∠C=180°，
∴∠C+∠CDE+∠E=360°，
∴∠C+∠CDE+∠E=2（∠A+∠B）．
解：∠C+∠D+∠E=2（∠A+∠B）．理由：过点D作DF∥AE，交AB于点F，
∵AE∥BC，
∴AE∥DF∥BC，
∴∠A+∠B=180°，∠E+∠EDF=180°，∠CDF+∠C=180°，
∴∠C+∠CDE+∠E=360°，
∴∠C+∠CDE+∠E=2（∠A+∠B）．
点评：此题考查了平行线的性质．此题比较适中，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
相关题目
某市在“旧城改造”中，计划在市内一块如图所示的三角形空地中种植草皮美化环境，已知这种草皮每平方米要80元，求买这种草皮至少需多少元．
如图，在△ABC中，AB=AC，AD⊥BC于点D，E是AD的中点，CE交AD边于点F，DG∥CF，交AB边于G．若AB=6，求线段AF的长．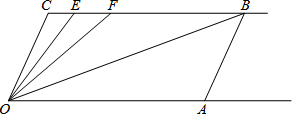
已知：如图，射线CB∥OA，∠C=∠OAB=120°，OE平分∠COF 交BC于点E，F在BC上，且满足OB平分∠AOF．
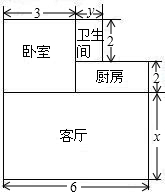大伟购买了一套经济适用房，户型图如图所示，请根据图中的数据（单位：m），解答下列问题：
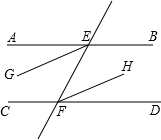如图所示，AB∥CD、EF分别交AB，CD于E、F，EG平分∠AEF，FH平分∠EFD，求证：EG∥FH．
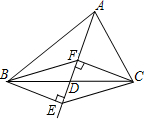如图，已知BE⊥AD，CF⊥AD，且BE=CF．