题目内容
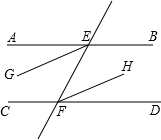 如图所示,AB∥CD、EF分别交AB,CD于E、F,EG平分∠AEF,FH平分∠EFD,求证:EG∥FH.
如图所示,AB∥CD、EF分别交AB,CD于E、F,EG平分∠AEF,FH平分∠EFD,求证:EG∥FH.证明:∵AB∥CD(已知)
∴∠AEF=∠EFD(
∵∠
| 1 |
| 2 |
| 1 |
| 2 |
∴∠
考点:平行线的判定与性质
专题:推理填空题
分析:根据平行线的性质得出∠AEF=∠EFD,根据角平分线定义得出∠GEF=
∠AEF,∠HFE=
∠EFD,求出∠GEF=∠HFE,根据平行线的判定推出即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵AB∥CD(已知),
∴∠AEF=∠EFD(两直线平行,内错角相等),
∵EG平分∠AEF,FH平分∠EFD,
∴∠GEF=
∠AEF,∠HFE=
∠EFD(角平分线定义),
∴∠GEF=∠HFE,
∵EG∥FH(内错角相等,两直线平行),
故答案为:两直线平行,内错角相等,GEF,HFE,GEF,HFE,内错角相等,两直线平行
∴∠AEF=∠EFD(两直线平行,内错角相等),
∵EG平分∠AEF,FH平分∠EFD,
∴∠GEF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠GEF=∠HFE,
∵EG∥FH(内错角相等,两直线平行),
故答案为:两直线平行,内错角相等,GEF,HFE,GEF,HFE,内错角相等,两直线平行
点评:本题考查了平行线的性质和判定,角平分线定义的应用,能正确运用性质进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
方程2-5x=9的解是( )
A、x=-
| ||
B、x=
| ||
C、x=
| ||
D、x=-
|
 把下列左圈中的每一个整式分别除以
把下列左圈中的每一个整式分别除以 (1)如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=40°,求∠BOC的度数;
(1)如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=40°,求∠BOC的度数; 已知DE∥BC,CD是∠ACB的角平分线,∠B=80°,∠ACB=50°,试求∠EDC与∠BDC的度数.
已知DE∥BC,CD是∠ACB的角平分线,∠B=80°,∠ACB=50°,试求∠EDC与∠BDC的度数. 如图,在五边形ABCDE中,AE∥BC,探索∠A+∠B与∠C+∠D+∠E的度数之间的数量关系,并说明理由.
如图,在五边形ABCDE中,AE∥BC,探索∠A+∠B与∠C+∠D+∠E的度数之间的数量关系,并说明理由. 如图,∠C=90°,∠BAC=30°,BC=1.将直角三角形纸片沿AD折叠,使点C落在AB上的点E处.求tan15°的值.
如图,∠C=90°,∠BAC=30°,BC=1.将直角三角形纸片沿AD折叠,使点C落在AB上的点E处.求tan15°的值. 如图,在五角星形中,C、D是AB的两个黄金分割点.若CD=1,则AB=
如图,在五角星形中,C、D是AB的两个黄金分割点.若CD=1,则AB=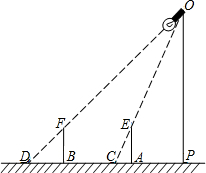 如图,小明准备用如下方法测量路灯的高度,他走到路灯旁的一个地方,竖起一根2m长的竹竿,测得竹竿影长为1m,他沿着影子的方向,又向远处走出两根竹竿的长度,他又竖起竹竿,测得影长正好为2m,路灯高度为多少米?
如图,小明准备用如下方法测量路灯的高度,他走到路灯旁的一个地方,竖起一根2m长的竹竿,测得竹竿影长为1m,他沿着影子的方向,又向远处走出两根竹竿的长度,他又竖起竹竿,测得影长正好为2m,路灯高度为多少米?