题目内容
7.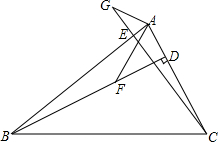 如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,F是BD上一点,BF=AC,G是CE延长线上一点,CG=AB,连接AG,AF.
如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,F是BD上一点,BF=AC,G是CE延长线上一点,CG=AB,连接AG,AF.(1)试说明∠ABD=∠ACE;
(2)探求线段AF,AG有什么关系?并请说明理由.
分析 (1)根据的等角的余角相等,即可证明∠ACG=∠ABF;
(2)根据SAS推出△ABF≌△GCA即可解决问题;
解答 (1)证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∴∠ABF+∠BAD=90°,∠GCA+∠BAD=90°,
∴∠ABF=∠GCA,
(2)结论:AF=AG,AF⊥AG.理由如下:
在△ABF和△GCA中,
$\left\{\begin{array}{l}{AB=CG}\\{∠ABF=∠GCA}\\{BF=AC}\end{array}\right.$,
∴△ABF≌△GCA(SAS),
∴AF=AG,∠GAC=∠AFB,
∵∠AFB=∠ADB+∠FAD,∠GAC=∠GAF+∠FAD,
∴∠GAF=∠ADF,
∵∠ADF=90°,
∴∠GAF=90°,
∴AG⊥AF,AG=AF.
点评 本题考查了三角形内角和定理,全等三角形的性质和判定的应用、同角的余角相等等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
18.若分式$\frac{1}{x+3}$的值大于0,则实数x的取值范围是( )
| A. | x>-3 | B. | x≥-3 | C. | x>3 | D. | x≠-3 |
2.列方程组解应用题:
在“某地大地震”灾民安置工作中,某企业捐助了一批板材24 000m2,某灾民安置点用该企业捐助的这批板材全部搭建成A,B两种型号的板房,供2 300名灾民临时居住.已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示:
问:(1)该灾民安置点需搭建A型板房和B型板房各多少间?
(2)因对灾民人数估计不足,实际安置中A型板房超员15%,B型板房超员20%,则该安置点灾民实际有多少人?
在“某地大地震”灾民安置工作中,某企业捐助了一批板材24 000m2,某灾民安置点用该企业捐助的这批板材全部搭建成A,B两种型号的板房,供2 300名灾民临时居住.已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示:
| 板房型号 | 所需板材 | 安置人数 |
| A型板房 | 54m2 | 5 |
| B型板房 | 78m2 | 8 |
(2)因对灾民人数估计不足,实际安置中A型板房超员15%,B型板房超员20%,则该安置点灾民实际有多少人?
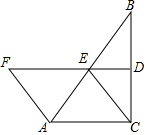 如图,∠ACB=90°,D,E分别为BC,AB的中点,DE的延长线交AF于F,∠F=∠FEA.
如图,∠ACB=90°,D,E分别为BC,AB的中点,DE的延长线交AF于F,∠F=∠FEA.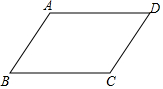 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,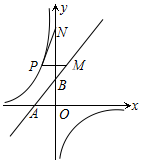 在平面直角坐标系中,已知点A(-$\sqrt{2}$,0)、B(0,$\sqrt{2}$)、N(0,3$\sqrt{2}$),P是反比例函数y=-$\frac{1}{x}$(x<0)的图象上一动点,PM∥x轴交直线AB于M,则PM+PN的最小值为$\frac{7\sqrt{2}}{3}$.
在平面直角坐标系中,已知点A(-$\sqrt{2}$,0)、B(0,$\sqrt{2}$)、N(0,3$\sqrt{2}$),P是反比例函数y=-$\frac{1}{x}$(x<0)的图象上一动点,PM∥x轴交直线AB于M,则PM+PN的最小值为$\frac{7\sqrt{2}}{3}$.
 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是1.
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是1.