题目内容
2.计算:(1)若 $\left\{\begin{array}{l}x-y=6\\ xy=-8\end{array}\right.$,求:
①(x+y)2的值;
②(x+2)(y-2)的值;
(2)若x2-x-4=0,计算x3+x2-6x的值.
分析 (1)①将(x+y)2化为(x-y)2+4xy可得结果;
②将(x+2)(y-2)化为xy-2(x-y)-4可得结果;
(2)先根据已知将x3+x2-6x降次可得结果.
解答 解:(1)①(x+y)2
=(x-y)2+4xy
=36-4×(-8)
=36+32
=68;
②(x+2)(y-2)
=xy-2(x-y)-4
=-8-2×6-4
=-24;
(2)∵x2-x-4=0,
∴x2=x+4,x2-x=4,
∴x3+x2-6x
=x(x+4)+x2-6x
=x2+4x+x2-6x
=2x2-2x
=2(x2-x)
=2×4
=8.
点评 本题主要考查了因式分解,多项式乘多项式等,将所求式子进行适当的变形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.如果∠A和∠B的两边分别平行,∠A=60°,那么∠B是( )
| A. | 60° | B. | 30°或120° | C. | 120° | D. | 60°或120° |
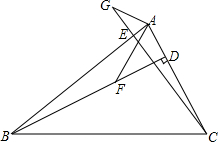 如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,F是BD上一点,BF=AC,G是CE延长线上一点,CG=AB,连接AG,AF.
如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,F是BD上一点,BF=AC,G是CE延长线上一点,CG=AB,连接AG,AF.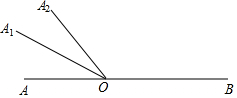 如图,点O是直线AB上一点,射线OA1,OA2均从OA的位置开始绕点O顺时针旋转,OA1旋转的速度为每秒30°,OA2旋转的速度为每秒10°.当OA2旋转6秒后,OA1也开始旋转,当其中一条射线与OB重合时,另一条也停止.设OA1旋转的时间为t秒.
如图,点O是直线AB上一点,射线OA1,OA2均从OA的位置开始绕点O顺时针旋转,OA1旋转的速度为每秒30°,OA2旋转的速度为每秒10°.当OA2旋转6秒后,OA1也开始旋转,当其中一条射线与OB重合时,另一条也停止.设OA1旋转的时间为t秒.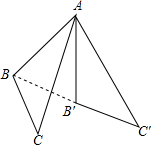 △ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB′C′,则∠BAB′的度数是60°.
△ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB′C′,则∠BAB′的度数是60°.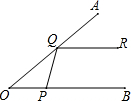 如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是100°.
如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是100°.