题目内容
11.定义感知:若抛物线的顶点为P,与y轴的交点为Q,则称直线PQ是该抛物线的“随形线”.初步运用:判断下列伦断是否正确?正确的在题后括号内打“√”,错误“×”;
1.对称轴不是y轴的抛物线有且只有一条“随形线”.(√)
2.抛物线y=x2-4x+2的“随形线”是直线y=2x+2.(×)
拓展延伸:若直线y=-3x+3是某抛物线的“随形线”,该“随形线”与y轴交于点Q,且抛物线顶点P与点Q相距2$\sqrt{10}$个单位长度.
(1)试求该抛物线的解析式;
(2)问所得到的抛物线能否经过适当的平移,才能使平移后的图象所对应的函数解析式为y=$\frac{3}{2}{x}^{2}$?若能,说明平移的方法;若不能,请说明理由.
分析 1.根据过抛物线的顶点与抛物线与y轴的交点有且只有一条直线,可得答案;
2.根据自变量与函数值的对应关系,可得抛物线与y轴的交点,根据配方法,可得顶点坐标,根据待定系数法,可得答案;
(1)根据“随形线”,可得抛物线与y轴的交点,根据交点与顶点的距离,可得顶点坐标,根据待定系数,可得函数解析式;
(2)根据函数解析式中a的值相同,函数图象可平移得到,根据函数图象的平移规律,可得答案.
解答 解:1.过两点有且只有一条直线,故对称轴不是y轴的抛物线有且只有一条“随形线”正确,(√)
2.y=x2-4x+2与y轴的交点坐标为(0,2)顶点坐标为(2,-2),
抛物线y=x2-4x+2的“随形线”是直线y=-2x+2.(×)
故答案为:√,×;
(1)当x=0时,y=3,即点Q的坐标为(0,3)设顶点P的坐标为(m,-3m+3),
由PQ=2$\sqrt{10}$,得m2+(3m-3+3)2=(2$\sqrt{10}$)2,
解得m1=2,m2=-2,
当m=2时,-3m+3=-3,即顶点P(2,-3);
当m=-2时,-3m+3=9,即顶点P的坐标为(-2,9).
当顶点(2,-3)时,设抛物线的解析式为y=a(x-2)2-3,
将Q(0,3)代入函数解析式,得4a-3=3,解得a=$\frac{3}{2}$,
当顶点(2,-3)时,设抛物线的解析式为y=$\frac{3}{2}$(x-2)2-3;
当顶点(-2,9)时,设抛物线的解析式为y=a(x+2)2+9,
将Q(0,3)代入函数解析式,得4a+9=3,解得a=-$\frac{3}{2}$,
当顶点(2,-3)时,设抛物线的解析式为y=-$\frac{3}{2}$(x-2)2-3;
综上所述:抛物线的解析式为y=$\frac{3}{2}$(x-2)2-3或y=-$\frac{3}{2}$(x-2)2-3;
(2)当抛物线的解析式为y=$\frac{3}{2}$(x-2)2-3时,可平移得到抛物线的解析式为y=$\frac{3}{2}$x2,
y=$\frac{3}{2}$(x-2)2-3的图象向左平移2个单位再向上平移3个单位得到抛物线的解析式为y=$\frac{3}{2}$x2;
当抛物线的解析式为y=-$\frac{3}{2}$(x-2)2-3时不能平移得到抛物线的解析式为y=$\frac{3}{2}$x2,理由如下:
a不同,抛物线的开口方向不同,形状不同,平移不能使抛物线重合.
点评 本题考查了二次函数综合题,利用了直线的性质,待定系数求函数解析式,把抛物线的解析式设成顶点式是解题关键,要分类讨论,以防遗漏.图象平移的规律是:左加右减,上加下减.

| A. | 正方形 | B. | 矩形 | ||
| C. | 菱形 | D. | 邻边相等的四边形 |
| A. | (a-b)2=a2-b2 | B. | (-a-b)2=a2+2ab-b2 | C. | (a+b)(a-b)=a2-b2 | D. | (a-b)2=a2-2ab-b2 |
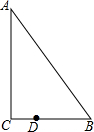 如图,Rt△ABC中,∠ACB=90°,∠B=50°,BC=3,且BD=2CD,将线段DB绕点D逆时针方向旋转至DB′,当点B′刚好旋转到△ABC的边上,且△DBB′为等腰三角形时旋转角的度数为80°或120°.
如图,Rt△ABC中,∠ACB=90°,∠B=50°,BC=3,且BD=2CD,将线段DB绕点D逆时针方向旋转至DB′,当点B′刚好旋转到△ABC的边上,且△DBB′为等腰三角形时旋转角的度数为80°或120°.
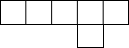 如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形).
如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形).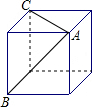 如图,在一个正方体的2个面上画了两条对角线AB、AC,那么这两条对角线的夹角是60°.
如图,在一个正方体的2个面上画了两条对角线AB、AC,那么这两条对角线的夹角是60°. 如图,在等腰△ABC中,AB=AC,BC边上的高AD=6cm,腰AB上的高CE=8cm,求BC2的值.
如图,在等腰△ABC中,AB=AC,BC边上的高AD=6cm,腰AB上的高CE=8cm,求BC2的值.