题目内容
6.在△ABC中,CO为AB边上的中线,且OC=$\frac{1}{2}$AB,以点O为圆心,OC长为半径画圆,延长CO交⊙O于点D,连结AD,BD,则四边形ADBC是( )| A. | 正方形 | B. | 矩形 | ||
| C. | 菱形 | D. | 邻边相等的四边形 |
分析 根据题意画出图形,根据对角线互相平分的四边形为平行四边形可得四边形ACBD是平行四边形,然后证明AB=CD,再根据对角线相等的平行四边形是矩形可得四边形ADBC为矩形.
解答  解:如图:
解:如图:
∵延长CO交⊙O于点D,
∴DO=CO,
∵CO为AB边上的中线,
∴AO=BO,
∴四边形ACBD是平行四边形,
∵OC=$\frac{1}{2}$AB,
∴AB=CD,
∴四边形ADBC为矩形,
故选:B.
点评 此题主要考查了矩形的判定,关键是掌握对角线相等的平行四边形是矩形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
16.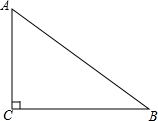 如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )
如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )
 如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )
如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
1.下列备选答案的四个数中,最小的一个是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
18.下面几个有理数最大的是( )
| A. | 2 | B. | 0 | C. | -3 | D. | -1 |
 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律大致如图所示(图中OABC为一折线),则这个容器的形状是( )
匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律大致如图所示(图中OABC为一折线),则这个容器的形状是( )


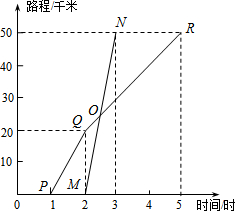 已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题:
已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题: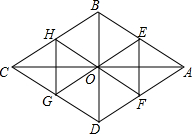 如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.
如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.