题目内容
1. 如图,在等腰△ABC中,AB=AC,BC边上的高AD=6cm,腰AB上的高CE=8cm,求BC2的值.
如图,在等腰△ABC中,AB=AC,BC边上的高AD=6cm,腰AB上的高CE=8cm,求BC2的值.
分析 根据三角形的面积公式求出$\frac{AB}{BC}$=$\frac{3}{4}$,根据等腰三角形的性质得到BD=DC=$\frac{1}{2}$BC,根据勾股定理列式计算即可.
解答 解:∵AD是BC边上的高,CE是AB边上的高,
∴$\frac{1}{2}$AB•CE=$\frac{1}{2}$BC•AD,
∵AD=6,CE=8,
∴$\frac{AB}{BC}$=$\frac{3}{4}$,
∴$\frac{A{B}^{2}}{B{C}^{2}}$=$\frac{9}{16}$,
∵AB=AC,AD⊥BC,
∴BD=DC=$\frac{1}{2}$BC,
∵AB2-BD2=AD2,
∴AB2=$\frac{1}{4}$BC2+36,
$\frac{9}{16}$BC2=$\frac{1}{4}$BC2+36,
解得:BC2=$\frac{576}{5}$.
点评 本题考查的是等腰三角形的性质、勾股定理的应用和三角形面积公式的应用,根据三角形的面积公式求出腰与底的比是解题的关键.

练习册系列答案
相关题目
9.下面的说法中,正确的是( )
| A. | -3和-1之间的有理数是-2 | |
| B. | 数轴上表示-a的点一定在原点的左边 | |
| C. | 在数轴上离开原点的距离越近的点表示的数越小 | |
| D. | -1和-2之间有无数个负数 |
3.下列各式中,能用平方差公式分解因式的是( )
| A. | x2+y2 | B. | x2-2x+1 | C. | -x2+y2 | D. | -x2-y2 |
 如图,在菱形ABCD中,∠A=60°,BD=5,则菱形ABCD的周长为20.
如图,在菱形ABCD中,∠A=60°,BD=5,则菱形ABCD的周长为20.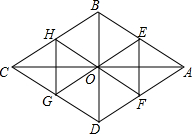 如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.
如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.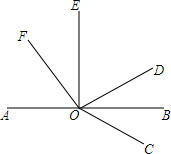 如图.点O是直线AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC.
如图.点O是直线AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC.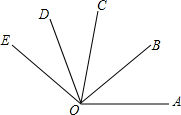 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,求∠BOD的度数.
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,求∠BOD的度数.