题目内容
3.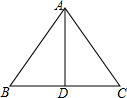 如图,在△ABC中,AB=10,BC=12,AD是BC边上的中线且AD=8.求证:△ABC是等腰三角形.
如图,在△ABC中,AB=10,BC=12,AD是BC边上的中线且AD=8.求证:△ABC是等腰三角形.
分析 在△ABD中,根据勾股定理的逆定理即可判断AD⊥BC,然后根据线段的垂直平分线的性质,即可得到AC=AB,从而求解.
解答 证明:∵AD是中线,AB=10,BC=12,AD=8,
∴BD=$\frac{1}{2}$BC=6.
∵62+82=102,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵BD=CD,
∴AC=AB,
∴△ABC是等腰三角形.
点评 本题主要考查了等腰三角形的判定,勾股定理的逆定理与线段的垂直平分线的性质,关键是利用勾股定理的逆定理证得AD⊥BC.

练习册系列答案
相关题目
8.一个等边三角形的边长为4,那么这个三角形的一条中位线长为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
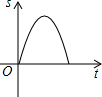
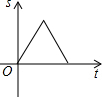
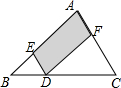 如图,在△ABC中,动点D从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动到点C(点D不与点B、C重合),运动时间为t,过点D作DE∥AC,DE∥AB,分别交AB于点E,交AC于点F,则图中阴影部分的面积S与时间t之间的函数图象大致为( )
如图,在△ABC中,动点D从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动到点C(点D不与点B、C重合),运动时间为t,过点D作DE∥AC,DE∥AB,分别交AB于点E,交AC于点F,则图中阴影部分的面积S与时间t之间的函数图象大致为( )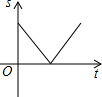
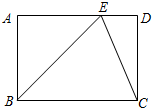 如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
如图,在矩形ABCD中,点E在AD上,EC平分∠BED. 已知:如图△ABC,∠ACB=2∠B=60°,BC=4.请按要求进行尺规作图,作∠ACB的平分线交AB于点D,再过点D作DE⊥BC,垂足为E,并求出AD的长.(不写作法,保留作图痕迹).
已知:如图△ABC,∠ACB=2∠B=60°,BC=4.请按要求进行尺规作图,作∠ACB的平分线交AB于点D,再过点D作DE⊥BC,垂足为E,并求出AD的长.(不写作法,保留作图痕迹).