题目内容
∠1的对顶角是∠2,∠2的邻补角是∠3,若∠3=75°,则∠1的度数是( )
| A、75° | B、105° |
| C、90° | D、75°或105° |
考点:对顶角、邻补角
专题:
分析:根据对顶角相等以及邻补角的关系进而得出∠1+∠3=180°,即可求出答案.
解答:解:∵∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=75°,
∴∠1=∠2,∠2+∠3=180°,
∴∠1+∠3=180°,
则∠1的度数是:180°-75°=105°.
故选:B.
∴∠1=∠2,∠2+∠3=180°,
∴∠1+∠3=180°,
则∠1的度数是:180°-75°=105°.
故选:B.
点评:此题主要考查了邻补角的定义以及对顶角性质,得出∠1+∠3=180°是解题关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 如图,将周长为24的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长( )
如图,将周长为24的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长( )| A、26 | B、28 | C、30 | D、48 |
有长度分别为4cm,8cm,10cm,12cm的四根木条,从中选出三根组成三角形,能组成( )个三角形.
| A、1 | B、2 | C、3 | D、4 |
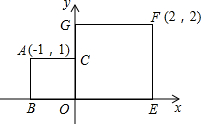 如图,点A坐标为(-1,1),点F坐标为(2,2),正方形ABOC沿x轴向右平移,若与正方形OEFG重叠部分面积为
如图,点A坐标为(-1,1),点F坐标为(2,2),正方形ABOC沿x轴向右平移,若与正方形OEFG重叠部分面积为| 1 |
| 2 |
A、(-
| ||||
B、(
| ||||
C、(-
| ||||
D、(
|
已知a>b,下列不等式中正确的是( )
| A、a+3<b+3 | ||||
| B、a-1<b-1 | ||||
| C、-a>-b | ||||
D、
|
八年级(1)班共有40名学生,其中22名男同学.本学期经班委讨论决定向希望工程捐款,已知男同学平均每人捐款2.5元,如果要使班级平均每人捐款达到2.8元,那么女同学平均每人至少捐款(精确到0.0l元)( )
| A、3元 | B、3.17元 |
| C、3.16元 | D、3.15元 |
 如图,m∥n,∠2=50°,那么∠1=
如图,m∥n,∠2=50°,那么∠1= 如图,在Rt△AOB中,∠O=90°,OA=1,OB=3;动点D从点O出发,以每秒1个单位长度的速度在线段OA上运动,当动点D到某一位置时,过点D作OA的垂线交线段AB于点N,设运动的时间为t秒,试问△AON能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
如图,在Rt△AOB中,∠O=90°,OA=1,OB=3;动点D从点O出发,以每秒1个单位长度的速度在线段OA上运动,当动点D到某一位置时,过点D作OA的垂线交线段AB于点N,设运动的时间为t秒,试问△AON能否为等腰三角形?若能,求出t的值;若不能,请说明理由.