题目内容
14.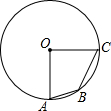 如图,已知A,B,C均在圆O上,且OA⊥OC,AB=1,BC=$\sqrt{2}$,则OABC的面积为$\frac{7}{4}$.
如图,已知A,B,C均在圆O上,且OA⊥OC,AB=1,BC=$\sqrt{2}$,则OABC的面积为$\frac{7}{4}$.
分析 连接OB,过点B作BH⊥AO于点H,作BI⊥OC于点I,如图所示,推出四边形OHBI是矩形,设OH=BI=a.BH=OI=b,OA=OC=R,根据勾股定理得到(R-a)2+b2=1 ①,(R-b)2+a2=2 ②,a2+b2=R2 ③,解方程即可得到结论.
解答 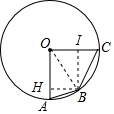 解:连接OB,过点B作BH⊥AO于点H,作BI⊥OC于点I,如图所示,
解:连接OB,过点B作BH⊥AO于点H,作BI⊥OC于点I,如图所示,
∵OA⊥OC,
∴四边形OHBI是矩形,
设OH=BI=a.BH=OI=b,OA=OC=R,
∴(R-a)2+b2=1 ①,
(R-b)2+a2=2 ②,
a2+b2=R2 ③,
由①、③得,2Ra=2R2-1,
∴a=R-$\frac{1}{2R}$ ④,
由②、③得,Rb=R2-1,
∴b=R-$\frac{1}{R}$ ⑤,
将④、⑤代入③得,R2+$\frac{5}{4{R}^{2}}$-3=0,∴4R4-12R2+5=0,解得R2=$\frac{5}{2}$,
将R2=$\frac{5}{2}$分别代入2Ra=2R2-1,Rb=R2-1得,Ra=2,Rb=$\frac{3}{2}$,
∴四边形OABC的面积=$\frac{1}{2}$Ra+$\frac{1}{2}$Rb=$\frac{7}{4}$.
故答案为:$\frac{7}{4}$.
点评 本题考查了垂径定理,矩形的性质,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
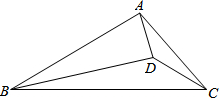 在△ABC中,AC=5$\sqrt{3}$,点D在三角形内部,连接AD、BD、CD,sin∠DCB=$\frac{1}{2}$,cos∠ABC=$\frac{\sqrt{3}}{2}$,BD=7$\sqrt{3}$,∠ABD=∠ACD,则线段AD的长度为2$\sqrt{3}$.
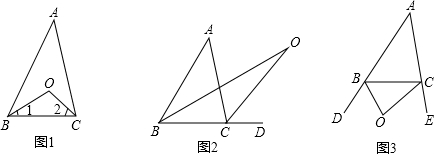
在△ABC中,AC=5$\sqrt{3}$,点D在三角形内部,连接AD、BD、CD,sin∠DCB=$\frac{1}{2}$,cos∠ABC=$\frac{\sqrt{3}}{2}$,BD=7$\sqrt{3}$,∠ABD=∠ACD,则线段AD的长度为2$\sqrt{3}$.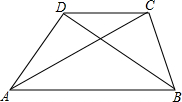 如图,已知梯形ABCD中,AB∥CD,AD>BC.求证:AC>BD.
如图,已知梯形ABCD中,AB∥CD,AD>BC.求证:AC>BD.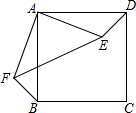 如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$.
如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$.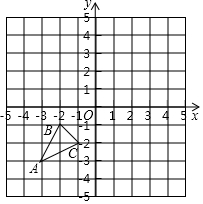 如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上三点.