题目内容
如图，四边形ABCD的对角线AC，BD交于点O，且OA=OC，OB=OD，则图中全等的三角形共有考点：全等三角形的判定
专题：
分析：利用平行四边形的对边平行且相等，对角线互相平分，对角相等可证出4组全等三角形．
解答：解：∵OA=OC，OB=OD，
∴四边形ABCD是平行四边形，
∴AB=CD，AD=BC，且AB∥CD，AD∥BC，∠ABC=∠CDA，∠BAD=∠DCB，
在△AOB和△COD中，
OA=OC，OB=OD，∠AOB=∠COD，
∴△AOB≌△COD，
同理可证△AOD≌△COB，
在△ABD和△CDB中，
AB=CD，∠BAC=∠DCB，AD=CB，
∴△ABD≌△CDB，
同理可证△ABC≌△DCA．
故答案是：4．
∴四边形ABCD是平行四边形，
∴AB=CD，AD=BC，且AB∥CD，AD∥BC，∠ABC=∠CDA，∠BAD=∠DCB，
在△AOB和△COD中，
OA=OC，OB=OD，∠AOB=∠COD，
∴△AOB≌△COD，
同理可证△AOD≌△COB，
在△ABD和△CDB中，
AB=CD，∠BAC=∠DCB，AD=CB，
∴△ABD≌△CDB，
同理可证△ABC≌△DCA．
故答案是：4．
点评：本题考查了平行四边形的性质和全等三角形的判定，解答本题的关键是熟练掌握全等三角形的判断，此题有一定的难度．
练习册系列答案
相关题目
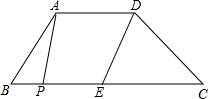如图，在四边形ABCD中，AD∥BC，E是BC的中点，AD=5，BC=12，点P是BC边上一动点．设PB的长为x．当x的值为
如图，△ABC是边长为1的等边三角形，取BC边中点E，作ED∥AB交AC于点D，EF∥AC交AB于点F，得到四边形EDAF，它的面积记做S1，取BE边中点E1，作E1D1∥FB交EF于点D1，E1F1∥EF交AB于点F1，得到四边形E1D1FF1，它的面积记做S2．照此规律作下去，则S2013=
如图，直线被a，b被c所截，a∥b，若∠2=135°，则∠1=
如图，在四边形ABCD中，E是BC边的中点，连接DE并延长，交AB的延长线于F点，AB=BF．添加一个条件，使四边形ABCD是平行四边形．你认为添加的条件可以是
如图，AB是半圆的直径，C，D是半圆上两个点，