Question

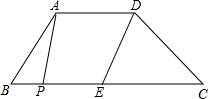如图，在四边形ABCD中，AD∥BC，E是BC的中点，AD=5，BC=12，点P是BC边上一动点．设PB的长为x．当x的值为

 

时，以点P，A，D，E为顶点的四边形为平行四边形．

Answer 1

考点：平行四边形的判定

专题：

分析：若以点P、A、D、E为顶点的四边形为平行四边形，那么AD=PE，有两种情况：①当P在E的左边，利用已知条件可以求出BP的长度；②当P在E的右边，利用已知条件也可求出BP的长度．

解答：若以点P、A、D、E为顶点的四边形为平行四边形，那么AD=PE，
有两种情况：①当P在E的左边，
∵E是BC的中点，
∴BE=6，
∴BP=BE-PE=6-5=1；
②当P在E的右边，
BP=BE+PE=6+5=11；
故当x的值为1或11时，以点P、A、D、E为顶点的四边形为平行四边形．
故答案是：1或11．

点评：本题考查了平行四边形的判定．解题时，要注意对点P的不同位置进行分类讨论，以防漏解．