题目内容
18.直角坐标系中点A关于y轴对称点为B(a,b),而点B关于x轴的对称点为C(-3,2),点A关于x轴的对称点为D.(1)试将A,B,C,D各点的纵坐标乘$\frac{1}{2}$,横坐标不变,求变化后相应的点A1,B1,C1,D1的坐标.
(2)请顺次连结A1,B1,C1,D1,求此四边形的面积.
分析 (1)根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可得A、B、C、D的坐标,然后再纵坐标乘$\frac{1}{2}$,横坐标不变可得点A1,B1,C1,D1的坐标;
(2)利用平面直角坐标系画出四边形A1B1C1D1,然后可得答案.
解答 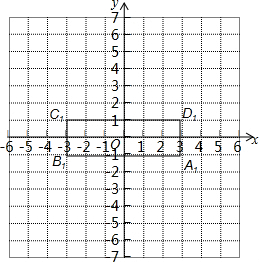 解:(1)∵点B关于x轴的对称点为C(-3,2),
解:(1)∵点B关于x轴的对称点为C(-3,2),
∴B(-3,-2),
∴a=-3,b=-2,
∴点A关于y轴对称点为B(-3,-2),
∴A(3,-2),
∵点A关于x轴的对称点为D,
∴D(3,2),
∵将A,B,C,D各点的纵坐标乘$\frac{1}{2}$,横坐标不变,
∴点A1(3,-1),B1(-3,-1),C1(-3,1),D1(3,1);
(2)四边形的面积:6×2=12.
点评 此题主要考查了关于x、y轴对称点的坐标,关键是掌握点的坐标的变化规律.

练习册系列答案
相关题目
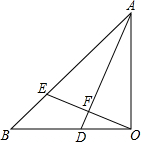 如图,△AOB中,OB=OA,∠AOB=90°,AD平分∠OAB交OB于D,OE⊥AD交AB于E,垂足为F,下列结论:
如图,△AOB中,OB=OA,∠AOB=90°,AD平分∠OAB交OB于D,OE⊥AD交AB于E,垂足为F,下列结论: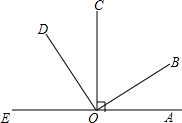 看图回答下列问题:
看图回答下列问题: 如图,点A、O、B在同一直线上,OC平分∠AOD,OE平分∠BOC,若∠COE=50°,求∠DOE的度数.
如图,点A、O、B在同一直线上,OC平分∠AOD,OE平分∠BOC,若∠COE=50°,求∠DOE的度数.