题目内容
9.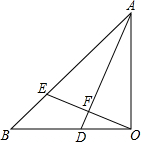 如图,△AOB中,OB=OA,∠AOB=90°,AD平分∠OAB交OB于D,OE⊥AD交AB于E,垂足为F,下列结论:
如图,△AOB中,OB=OA,∠AOB=90°,AD平分∠OAB交OB于D,OE⊥AD交AB于E,垂足为F,下列结论:①OF=EF;②OB=BE;③AB=OB+OD;④AD-OE=2DF,
其中正确的有( )
| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
分析 由已知条件和三角形内角和定理证出∠AEO=∠AOE,得出AE=AO,由等腰三角形的三线合一性质得出OF=EF,①正确;由大角对大边得出②不正确;
证出DE=DO,BE=DE,得出③正确;在AF上截取FM=DF,连接OM,由ASA证明△AOM≌△OBE,得出AM=OE,得出AD-OE=2DF,④正确;即可得出结论.
解答 解:∵AD平分∠OAB,OE⊥AD,
∴∠EAF=∠OAF,∠AFE=∠AFO=90°,
∴∠AEO=∠AOE,
∴AE=AO,
∴OF=EF,①正确;
∵∠BEO>∠BOE,
∴OB>BE,②不正确;
连接DE,如图1所示: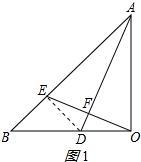
∵AE=AO,∠AEO=∠AOE,
∵AD⊥OE,EF=FO,
∴DE=DO,
∴∠DEO=∠DOE,
∵∠AEO=∠AOE,
∴∠AED=∠AOB=90°,
∵∠AOB=90°,AO=BO,
∴∠B=45°,
∴∠EDB=∠AEO-∠B=90°-45°=45°=∠B,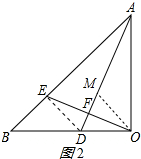
∴BE=DE,
∴OD=BE,③正确.
在AF上截取FM=DF,连接OM,如图2所示:
∵OB=OA,∠AOB=90°,
∴∠B=∠OAB=45°,
∵AD平分∠OAB,
∴∠EAF=∠OAF=22.5°,
∵AD⊥OE,
∴∠DOF=∠OAF=22.5°,
∵FM=DF,
∴OM=OD,
∴∠MOF=∠DOF=22.5°,
∴∠DOM=45°,
∴∠AOM=45°,
在△AOM和△OBE中,
$\left\{\begin{array}{l}{∠OAM=∠BOE}&{\;}\\{OA=OB}&{\;}\\{∠AOM=∠B}&{\;}\end{array}\right.$,
∴△AOM≌△OBE(ASA),
∴AM=OE,
∴AD-OE=AD-AM=DM=2DF,④正确;
正确的是①③④;
故选:B.
点评 本题考查了角平分线、等腰直角三角形的性质、全等三角形的判定与性质、线段垂直平分线的性质、等腰三角形的判定与性质等知识;本题综合性强,有一定难度.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| 每季度用水吨数 | 收费标准 |
| 不超过10吨 | 2.5元/吨 |
| 超过10吨,但不超过15吨 | 3元/吨 |
| 超过15吨 | 4元/吨 |
(2)城市为提倡居民节约用水,决定采取用水打折优惠的方法鼓励居民节约用水,优惠政策如下:
①每季度用水不超过10吨,每吨水打八折;
②每季度用水超过10吨,但不超过15吨,每吨水打九折;
③每季度用水超过15吨,每吨水收费比原价多收10%.
小智家某季度实际交费35.1元,求小智家这季度用水多少吨.
(3)在(2)的条件下,已知小智家第三季度节省4.8元,第四季度节省4.2元,小智家第三、四季度共用水多少吨?
 如图,△ABC为等边三角形,以AB为边向△ABC外侧作△ABD,使得∠ADB=120°,再以点C为旋转中心把△CBD沿着顺时针旋转至△CAE,则下列结论:
如图,△ABC为等边三角形,以AB为边向△ABC外侧作△ABD,使得∠ADB=120°,再以点C为旋转中心把△CBD沿着顺时针旋转至△CAE,则下列结论: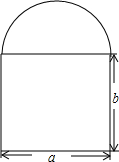 如图所示是某建筑物的窗户,上半部分为半圆形,下半部分为长方形,已知长方形的长,宽分别为a,b,这扇窗户的透光面积是$\frac{1}{8}$πa2+ab.
如图所示是某建筑物的窗户,上半部分为半圆形,下半部分为长方形,已知长方形的长,宽分别为a,b,这扇窗户的透光面积是$\frac{1}{8}$πa2+ab. 如图,用图中的字母表示图中阴影部分的面积是ax+2bx(不能带括号).
如图,用图中的字母表示图中阴影部分的面积是ax+2bx(不能带括号).