题目内容
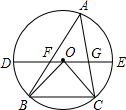如图，△ABC为⊙O的内接三角形，∠A=60°，直径DE∥BC，AB、AC分别与DE相交于点F、G，若⊙O的半径为2，则线段FG的最大值为考点：相似三角形的判定与性质,垂径定理
专题：
分析：过O作OJ⊥BC交点J，利用垂径定理可求得BC的长，连接AO并延长交BC于点H，则可得
=
=
，所以可知当OH最小时FG有最大值，即OH=OJ时FG有最大值，代入可得出答案．
| FG |
| BC |
| AO |
| AH |
| AO |
| AO+OH |
解答：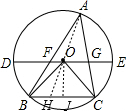
解：如图，过O作OJ⊥BC交点J，连接AO并延长交BC于点H，
∵∠A=60°，
∴∠BOC=120°，
∴∠OBJ=30°，且OB=2，
∴OJ=1，BJ=CJ=
，
∴BC=2
，
∵DE∥BC，
∴
=
=
，即
=
，
∴FG=
，
∴当OH最小时FG有最大值，即OH=OJ=1时FG有最大值，
此时FG=
，
故答案为：
．
解：如图，过O作OJ⊥BC交点J，连接AO并延长交BC于点H，∵∠A=60°，
∴∠BOC=120°，
∴∠OBJ=30°，且OB=2，
∴OJ=1，BJ=CJ=
| 3 |
∴BC=2
| 3 |
∵DE∥BC，
∴
| FG |
| BC |
| AO |
| AH |
| AO |
| AO+OH |
| FG | ||
2
|
| 2 |
| 2+OH |
∴FG=
4
| ||
| 2+OH |
∴当OH最小时FG有最大值，即OH=OJ=1时FG有最大值，
此时FG=
4
| ||
| 3 |
故答案为：
4
| ||
| 3 |
点评：本题主要考查平行线分线段成比例，利用条件把FG用OH表示出来，判断出何时FG有最大值是解题的关键．
练习册系列答案
相关题目
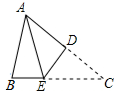如图，将三角形纸片ABC折叠，使点C与点A重合，折痕为DE．若∠B=82°，∠BAE=26°，则∠EAD的度数为（ ）| A、28° | B、30° |
| C、36° | D、45° |
如图，是一个风筝的图案，它是轴对称图形，EF是对称轴，∠A=90°，∠AED=120°，∠C=50°，则∠BFC的度数为
已知：如图，A、C、F、D在同一直线上，AF=CD，AB=DE，BC=EF，求证：∠B=∠E．化简x÷
•
结果是（ ）
| x |
| y |
| 1 |
| x |
| A、1 | ||
| B、xy | ||
C、
| ||
D、
|
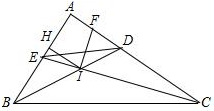如图，△ABC中，∠A=90°，角平分线BD、CE交于点I，IF⊥CE交CA于F，IH⊥AB于H，下列结论：①∠DIF=45°；②CF+BE=BC；③AE+AF=2AH；④S四边形△BEDC=2S△IBC，其中正确结论的个数为（ ）