Question

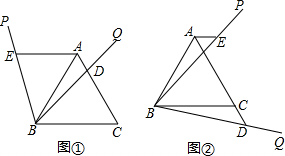探究：如图①，△ABC是等边三角形，以点B为顶点作∠PBQ=60°，BQ交边AC于点D，过点A作AE∥BC，AE交BP于点E．
求证：AD+AE=AB；
应用：在图①的基础上，将∠PBQ绕着点B顺时针旋转，如图②，使BQ交AC的延长线于点D，BP交边AC于点G．若AB=8，AE=2，则GD的长为

 

．

Answer 1

考点：全等三角形的判定与性质,等边三角形的性质

专题：

分析：探究：证△ABE≌△CBD，然后根据等边三角形三边相等即可求得．
应用：由探究可知AE=CD，然后平行线分线段成比例定理即可求得．

解答：探究：证明：∵△ABC是等边三角形，
∴∠ABC=∠ACB=60°，AB=BC，
∵∠PBQ=60°，
∴∠ABC-∠ABQ=∠PBQ-∠ABQ，
即∠ABE=∠CBD．
∵AE∥BC，
∴∠EAB=∠ABC=60°，
∴∠EAB=∠ACB，
在△ABE与△CBD中

∠ABE=∠CBD AB=BC ∠EAB=∠ACB

∴△ABE≌△CBD，
∴AE=CD．
∵AC=AD+CD，
∵AC=AB，
∴AD+AE=AB．        

应用：解：∵AE∥BC，
∴

AE

BC

=

AG

GC

=

AG

AC-AG

，
∴

2

8

=

AG

8-AG

，
解得：AG=1.6，
由探究可知△ABE≌△CBD，
∴AE=CD．
∴AD=AC+CD=10，
∴GD=10-1.6=8.4．

点评：本题考查了等边三角形的性质、全等三角形的判定和性质，以及平行线分线段定理的应用．