题目内容
已知k是一元二次方程x2-3x+1=0的一个根,求k2-2k+
的值.
| 3 |
| k2+1 |
考点:一元二次方程的解
专题:
分析:将x=k代入方程得到k2-3k+1=0,即k2=3k-1,k2+1=3k,再由根与系数的关系可得方程的另一根为
,k+
=3.然后将k2-2k+
变形为k-1+
,代入即可求解.
| 1 |
| k |
| 1 |
| k |
| 3 |
| k2+1 |
| 1 |
| k |
解答:解:∵k是一元二次方程x2-3x+1=0的一个根,
∴k2-3k+1=0,
∴k2=3k-1,k2+1=3k.
设方程的另一根为x2,由根与系数的关系可得
k+x2=3,k•x2=1,
∴x2=
,k+
=3.
∴k2-2k+
=3k-1-2k+
=k-1+
=3-1=2.
∴k2-3k+1=0,
∴k2=3k-1,k2+1=3k.
设方程的另一根为x2,由根与系数的关系可得
k+x2=3,k•x2=1,
∴x2=
| 1 |
| k |
| 1 |
| k |
∴k2-2k+
| 3 |
| k2+1 |
| 3 |
| 3k |
| 1 |
| k |
点评:此题考查了一元二次方程的解,根与系数的关系以及代数式的求值,利用了整体代入的数学思想,其中方程的解为:能使方程左右两边相等的未知数的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
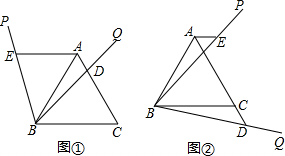 探究:如图①,△ABC是等边三角形,以点B为顶点作∠PBQ=60°,BQ交边AC于点D,过点A作AE∥BC,AE交BP于点E.
探究:如图①,△ABC是等边三角形,以点B为顶点作∠PBQ=60°,BQ交边AC于点D,过点A作AE∥BC,AE交BP于点E. 如图,在△ABC中,点O在AB边上,过点O作BC的平行线交∠ABC的平分线于点D,过点B作BE⊥BD交直线OD于点E.
如图,在△ABC中,点O在AB边上,过点O作BC的平行线交∠ABC的平分线于点D,过点B作BE⊥BD交直线OD于点E. 如图,已知四边形ABCD四个顶点的坐标为A(1,3),B(m,0),C(m+2,0),D(5,1),当四边形ABCD的周长最小时,m的值为
如图,已知四边形ABCD四个顶点的坐标为A(1,3),B(m,0),C(m+2,0),D(5,1),当四边形ABCD的周长最小时,m的值为