题目内容
若19a2+99a+1=0,b2+99b+19=0,求
(ab≠1).
| ab+4a+1 |
| b |
考点:根与系数的关系
专题:
分析:由已知条件可知a与
是一元二次方程19x2+99x+1=0的两个根,再根据根与系数的关系得出a+
=-
,a•
=
,代入所求代数式计算即可求解.
| 1 |
| b |
| 1 |
| b |
| 99 |
| 19 |
| 1 |
| b |
| 1 |
| 19 |
解答:解:∵b2+99b+19=0,ab≠1,
∴b≠0,将方程两边同时除以b2,得19(
)2+99(
)+1=0,
∵19a2+99a+1=0,
∴a与
是一元二次方程19x2+99x+1=0的两个根,
∴a+
=-
,a•
=
,
∴
=a+
+4a•
=-
+
=-
.
∴b≠0,将方程两边同时除以b2,得19(
| 1 |
| b |
| 1 |
| b |
∵19a2+99a+1=0,
∴a与
| 1 |
| b |
∴a+
| 1 |
| b |
| 99 |
| 19 |
| 1 |
| b |
| 1 |
| 19 |
∴
| ab+4a+1 |
| b |
| 1 |
| b |
| 1 |
| b |
| 99 |
| 19 |
| 1 |
| 19 |
| 98 |
| 19 |
点评:本题考查了一元二次方程的解的定义及根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,则x1+x2=-
,x1x2=
.得出a与
是一元二次方程19x2+99x+1=0的两个根是解题的关键.
| b |
| a |
| c |
| a |
| 1 |
| b |

练习册系列答案
相关题目
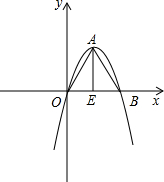 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.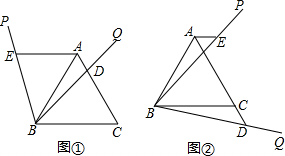 探究:如图①,△ABC是等边三角形,以点B为顶点作∠PBQ=60°,BQ交边AC于点D,过点A作AE∥BC,AE交BP于点E.
探究:如图①,△ABC是等边三角形,以点B为顶点作∠PBQ=60°,BQ交边AC于点D,过点A作AE∥BC,AE交BP于点E. 如图,在△ABC中,点O在AB边上,过点O作BC的平行线交∠ABC的平分线于点D,过点B作BE⊥BD交直线OD于点E.
如图,在△ABC中,点O在AB边上,过点O作BC的平行线交∠ABC的平分线于点D,过点B作BE⊥BD交直线OD于点E. 如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,连结A1B1,A2B2,…,An-1Bn-1,分别交曲线y=
如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,连结A1B1,A2B2,…,An-1Bn-1,分别交曲线y=