题目内容
解下列方程(组):
(1)
;
(2)
-
=-3.
(1)
|
(2)
| x-5 |
| x2-1 |
| 2 |
| 1-x |
考点:解分式方程
专题:计算题
分析:(1)方程组第一个方程变形表示出y,代入第二个方程,消去y求出x的值,进而求出y的值,即可确定出方程组的解;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答:解:(1)
,
由①得:y=17-x,
代入②得:x2+(17-x)2=169,
整理得:x2-17x+60=0,
即(x-5)(x-12)=0,
解得:x=5或x=12,
将x=5代入得:y=12;将x=12代入得:y=5,
则方程组的解为
或
;
(2)去分母得:x-5+2x+2=-3x2+3,
整理得:x2+x-2=0,即(x-1)(x+2)=0,
解得:x=1或x=-2,
经检验x=1是增根,分式方程的解为x=-2.
|
由①得:y=17-x,
代入②得:x2+(17-x)2=169,
整理得:x2-17x+60=0,
即(x-5)(x-12)=0,
解得:x=5或x=12,
将x=5代入得:y=12;将x=12代入得:y=5,
则方程组的解为
|
|
(2)去分母得:x-5+2x+2=-3x2+3,
整理得:x2+x-2=0,即(x-1)(x+2)=0,
解得:x=1或x=-2,
经检验x=1是增根,分式方程的解为x=-2.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
正比例函数y=6x的图象与反比例函数y=
的图象的交点位于( )
| 6 |
| x |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第一、三象限 |
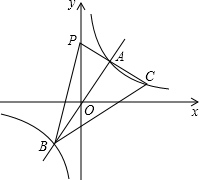 如图,在平面直角坐标系xOy中,直线y=
如图,在平面直角坐标系xOy中,直线y=
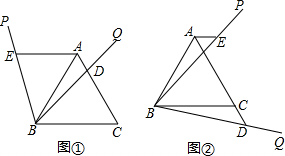 探究:如图①,△ABC是等边三角形,以点B为顶点作∠PBQ=60°,BQ交边AC于点D,过点A作AE∥BC,AE交BP于点E.
探究:如图①,△ABC是等边三角形,以点B为顶点作∠PBQ=60°,BQ交边AC于点D,过点A作AE∥BC,AE交BP于点E.