题目内容
15.△ABC中,∠ACB=60°,AE,BD是△ABC的角平分线,AE,BD交于点O.(1)求∠AOB的度数;
(2)求证:OD=OE.
分析 (1)根据内心的概念和角平分线的性质、结合三角形内角和定理计算即可;
(2)作OG⊥BC于G,OH⊥AC于H,证明△OHG≌△OGD即可.
解答 (1)解: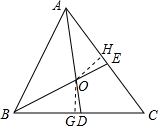 ∵∠ACB=60°,
∵∠ACB=60°,
∴∠CAB+∠CBA=120°,
∵AE,BD是△ABC的角平分线,
∴∠OAB=$\frac{1}{2}$∠CAB,∠OBA=$\frac{1}{2}$∠CBA,
∴∠AOB=180°-(∠OAB+∠OBA)
=180°-$\frac{1}{2}$(∠CAB+∠CBA)=120°;
(2)证明:作OG⊥BC于G,OH⊥AC于H,
∵∠ACB=60°,OG⊥BC,OH⊥AC,
∴∠GOH=120°,又∠AOB=120°,
∴∠GOD=∠HOE,
∵AE,BD是△ABC的角平分线,AE,BD交于点O,
∴CO是∠BCA的平分线,OG⊥BC,OH⊥AC,
∴OG=OH,
在△OHG和△OGD中,
$\left\{\begin{array}{l}{∠GOD=∠HOE}\\{∠OGD=∠OHE}\\{OG=OH}\end{array}\right.$,
∴△OHG≌△OGD,
∴OD=OE.
点评 本题考查的是角平分线的性质、全等三角形的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 已知:如图所示,在△ABC中,AB=AC,D为CA延长线上一点,DE⊥BC,交AB于点F.求证:∠D=∠AFD.
已知:如图所示,在△ABC中,AB=AC,D为CA延长线上一点,DE⊥BC,交AB于点F.求证:∠D=∠AFD. 如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要( )
如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要( )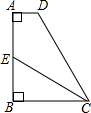 如图,在四边形ABCD中,AD∥BC,AB⊥AD,CE平分∠DCB交AB于E,点E是AB的中点.
如图,在四边形ABCD中,AD∥BC,AB⊥AD,CE平分∠DCB交AB于E,点E是AB的中点. 如图,在直角三角形ABC中,∠BAC=90°,作BC边上的高AD,图中出现多少个直角三角形?又作△ABD中AB边上的高DD1,这时,图中共出现多少个直角三角形?按照同样的方法作下去,作D1D2,D2D3,…,当作出Dn-1Dn时,图中共出现多少个直角三角形?
如图,在直角三角形ABC中,∠BAC=90°,作BC边上的高AD,图中出现多少个直角三角形?又作△ABD中AB边上的高DD1,这时,图中共出现多少个直角三角形?按照同样的方法作下去,作D1D2,D2D3,…,当作出Dn-1Dn时,图中共出现多少个直角三角形?