题目内容
6.已知实数x,y满足x2+y2-4x-2y+5=0,求$\frac{\sqrt{x}-y}{\sqrt{3y-2\sqrt{x}}}$的值.分析 根据x2+y2-4x-2y+5=0,可以求得x、y的值,从而可以求得$\frac{\sqrt{x}-y}{\sqrt{3y-2\sqrt{x}}}$的值.
解答 解:∵x2+y2-4x-2y+5=0,
∴x2-4x+4+y2-2y+1=0,
∴(x-2)2+(y-1)2=0,
∴x-2=0且y-1=0,
解得x=2,y=1,
∴$\frac{\sqrt{x}-y}{\sqrt{3y-2\sqrt{x}}}$
=$\frac{\sqrt{2}-1}{\sqrt{3×1-2\sqrt{2}}}$
=$\frac{\sqrt{2}-1}{\sqrt{2-2\sqrt{2}+1}}$
=$\frac{\sqrt{2}-1}{\sqrt{(\sqrt{2}-1)^{2}}}$
=$\frac{\sqrt{2}-1}{\sqrt{2}-1}$
=1.
点评 本题考查二次根式的化简求值,解题的关键是求出x、y的值.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目

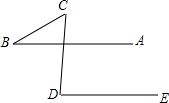 如图,AB∥ED,试直接写出∠B,∠C,∠D三者之间的数量关系.
如图,AB∥ED,试直接写出∠B,∠C,∠D三者之间的数量关系.