题目内容
课外阅读课上,老师将43本书分给各小组,每组8本,还有剩余;每组9本却又不够,问有几个小组?
 x=5.
【解析】试题分析:根据题意中的不等关系,设有x个小组,列不等式组求解,然后判断出正整数解即可.
试题解析:设有x个小组,题意得,解得:<x<,因为x为正整数,所以x=5.
x=5.
【解析】试题分析:根据题意中的不等关系,设有x个小组,列不等式组求解,然后判断出正整数解即可.
试题解析:设有x个小组,题意得,解得:<x<,因为x为正整数,所以x=5.
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
如果△ABC中,两边a=7cm,b=3cm,则c的取值范围是_________;第三边为奇数的所有可能值为_________;周长为偶数的所有可能值为_________.
 4cm<c<10cm 5cm、7cm、9cm 16cm或18cm
【解析】根据三角形的三边关系,得7cm?3cm
4cm<c<10cm 5cm、7cm、9cm 16cm或18cm
【解析】根据三角形的三边关系,得7cm?3cm如图所示的抛物线是二次函数y= +bx+c(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b,其中正确的结论有( ).
+bx+c(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b,其中正确的结论有( ).
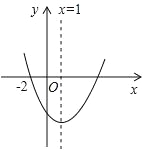
A.1个 B.2个 C.3个 D.4个
 C.
【解析】
试题分析:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x==1,∴b=﹣2a<0,所以②正确;∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以①正确;∵点(﹣2,0)关于直线x=1的对称点的坐标为(4,0),∴抛物线与x轴的另一个交点坐标为(4,0),所以③正确;∵x=﹣1时,y<0,
即a﹣b+c<0,∴a+c<b,所以④错误.
故选:C...
C.
【解析】
试题分析:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x==1,∴b=﹣2a<0,所以②正确;∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以①正确;∵点(﹣2,0)关于直线x=1的对称点的坐标为(4,0),∴抛物线与x轴的另一个交点坐标为(4,0),所以③正确;∵x=﹣1时,y<0,
即a﹣b+c<0,∴a+c<b,所以④错误.
故选:C... 如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A﹣B﹣M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( ).
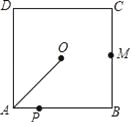
A. 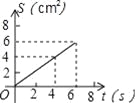 B.
B. 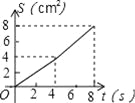
C. 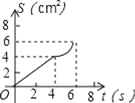 D.
D. 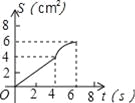
 A
【解析】试题分析:分两种情况:①当0≤t<4时,作OG⊥AB于G,如图1所示,由正方形的性质得出∠B=90°,AD=AB=BC=4cm,AG=BG=OG=AB=2cm,由三角形的面积得出S=AP•OG=t();②当t≥4时,作OG⊥AB于G,如图2所示,S=△OAG的面积+梯形OGBP的面积=×2×2+(2+t﹣4)×2=t();综上所述:面积S()与时间t(s)的关系的图象是过原点的线...
A
【解析】试题分析:分两种情况:①当0≤t<4时,作OG⊥AB于G,如图1所示,由正方形的性质得出∠B=90°,AD=AB=BC=4cm,AG=BG=OG=AB=2cm,由三角形的面积得出S=AP•OG=t();②当t≥4时,作OG⊥AB于G,如图2所示,S=△OAG的面积+梯形OGBP的面积=×2×2+(2+t﹣4)×2=t();综上所述:面积S()与时间t(s)的关系的图象是过原点的线... 下列关于函数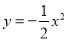 的图象说法:①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点(0,0),其中正确的有( )
的图象说法:①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点(0,0),其中正确的有( )
A.1个 B.2个 C.3个 D.4个
 D
【解析】
试题分析:函数是一种最基本的二次函数,画出图象,直接可知:
② 二次函数的图象是抛物线,正确;
②因为a=﹣<0,抛物线开口向下,正确;
③因为b=0,对称轴是y轴,正确;
④顶点(0,0)也正确.
故选D.
D
【解析】
试题分析:函数是一种最基本的二次函数,画出图象,直接可知:
② 二次函数的图象是抛物线,正确;
②因为a=﹣<0,抛物线开口向下,正确;
③因为b=0,对称轴是y轴,正确;
④顶点(0,0)也正确.
故选D. 如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x+b>kx+6的解集是_____.
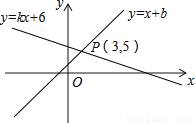
 x>3.
【解析】试题解析:当x>3时,x+b>kx+6,
即不等式x+b>kx+6的解集为x>3.
x>3.
【解析】试题解析:当x>3时,x+b>kx+6,
即不等式x+b>kx+6的解集为x>3. 下列结论中,正确的是( )
A. 若a>b,则 <
<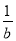 B. 若a>b,则a2>b2
B. 若a>b,则a2>b2
C. 若a>b,则1-a<1-b D. 若a>b,ac2>bc2
 C
【解析】当1>a>b>0时, <,故不正确;当a>0,b<0,a<|b|时,a2<b2,故不正确;由a>b可知-a<-b,因此可得1-a<1-b,故正确;当c=0时,虽然a>b,但是ac2=bc2=0,故不正确.
故选:C.
C
【解析】当1>a>b>0时, <,故不正确;当a>0,b<0,a<|b|时,a2<b2,故不正确;由a>b可知-a<-b,因此可得1-a<1-b,故正确;当c=0时,虽然a>b,但是ac2=bc2=0,故不正确.
故选:C. 在□ABCD中,对角线AC,BD相交于O点,AC=10,BD=8,则AD长的取值范围是 ( )
A. AD>1 B. AD<9 C. 1<AD<9 D. AD>10
 C
【解析】【解析】
平行四边形的对角线互相平分得:两条对角线的一半分别是5,4.再根据三角形的三边关系,得:1<AD<9.故选C.
C
【解析】【解析】
平行四边形的对角线互相平分得:两条对角线的一半分别是5,4.再根据三角形的三边关系,得:1<AD<9.故选C. 若不等式(a-2)x>a-2可以变形为x<1,则a的取值范围为_____.
 a<2
【解析】根据一元一次不等式的解法和基本性质,可由(a-2)x>a-2的解集为x<1,可知a-2<0,解得a<2.
故答案为:a<2.
a<2
【解析】根据一元一次不等式的解法和基本性质,可由(a-2)x>a-2的解集为x<1,可知a-2<0,解得a<2.
故答案为:a<2. 
