题目内容
17.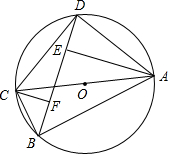 如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.
如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.(1)求证:BF=DE;
(2)若DE=2,AE=6,DF=12.求⊙O的直径.
分析 (1)证明:延长CF交⊙O于H,连接AH,作OM⊥BD于M,延长MO交AH于N,如图,由垂径定理得BM=DM,再由圆周角定理得到∠AHC=90°,易得四边形AHFE为矩形,接着证明M点为EF的中点得到FM=EM,则BF=DE;
(2)解:易得四边形ANME为矩形,则MN=AE=6,BF=2,EF=10,BE=7,AH=EF=10,利用勾股定理计算出AD=2$\sqrt{10}$,AB=$\sqrt{85}$,然后证明Rt△ACB∽Rt△ADE,再利用相似比计算出AC即可.
解答 (1)证明:延长CF交⊙O于H,连接AH,作OM⊥BD于M,延长MO交AH于N,如图,
∵OM⊥BD,
∴BM=DM,
∵AC为直径,
∴∠AHC=90°,
∵AE⊥BD于E,CF⊥BD,
∴四边形AHFE为矩形,MN∥AE∥FH,
∵ON∥CH,点O为AC的中点,
∴点N为AH的中点,
∴M点为EF的中点,
∴FM=EM,
∴BM-FM=DM-EM,
即BF=DE;
(2)解:易得四边形ANME为矩形,则MN=AE=6,
∵DE=2,DF=12,
∴BF=2,EF=12-2=10,BE=7,
∴AH=EF=10,
在Rt△ADE中,AD=$\sqrt{D{E}^{2}+A{E}^{2}}$=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$,
在Rt△ABE中,AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{{6}^{2}+{7}^{2}}$=$\sqrt{85}$,
∵AC为直径,
∴∠ABC=90°,
∵∠ACB=∠ADE,
∴Rt△ACB∽Rt△ADE,
∴$\frac{AC}{AD}$=$\frac{AB}{AE}$,即$\frac{AC}{2\sqrt{10}}$=$\frac{\sqrt{85}}{6}$,解得AC=$\frac{5\sqrt{34}}{3}$,
即圆的直径为$\frac{5\sqrt{34}}{3}$.
点评 本题考查了圆内接四边形的性质:圆内接四边形的对角互补.也考查了圆周角定理和相似三角形的判定与性质.

 阅读快车系列答案
阅读快车系列答案| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y2>y3>y1 | D. | y2<y3<y1 |
| A. | m=$\frac{1}{2}$n | B. | m=$\frac{1}{4}$n | C. | m=$\frac{1}{2}$n2 | D. | m=$\frac{1}{4}$n2 |
| A. | -a2+b2 | B. | 16m2-25m4 | C. | 2x2-$\frac{1}{2}$y2 | D. | -4x2-9 |
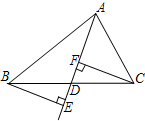 如图,已知BE⊥AD,CF⊥AD,BE=CF,由这三个条件组合运用可以得到若干结论,请你写出三个正确结论:△BDE≌△CDF,BD=CD,AD是△ABC的中线.
如图,已知BE⊥AD,CF⊥AD,BE=CF,由这三个条件组合运用可以得到若干结论,请你写出三个正确结论:△BDE≌△CDF,BD=CD,AD是△ABC的中线.
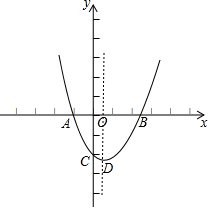 在平面直角坐标系中(如图),已知抛物线y=x2+bx+c与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-2).
在平面直角坐标系中(如图),已知抛物线y=x2+bx+c与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-2).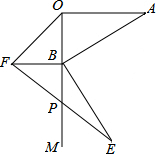 如图,AO⊥OM,OA=8$\sqrt{2}$,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度为4$\sqrt{2}$.
如图,AO⊥OM,OA=8$\sqrt{2}$,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度为4$\sqrt{2}$.