题目内容
5.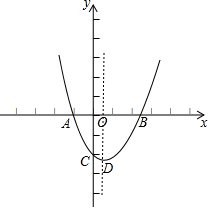 在平面直角坐标系中(如图),已知抛物线y=x2+bx+c与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-2).
在平面直角坐标系中(如图),已知抛物线y=x2+bx+c与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-2).(1)求该抛物线的表达式,并写出其对称轴;
(2)点D为该抛物线的顶点,设点P(t,0),且t>3,如果△BDP和△CDP的面积相等,求t的值.
分析 (1)把A点和C点坐标代入y=x2+bx+c得到关于b、c的方程,然后解方程求出b、c即可;
(2)先利用二次函数的性质求出D($\frac{1}{2}$,-$\frac{9}{4}$),再利用抛物线与x轴的交点问题求出B(2,0),则可根据待定系数法求出直线BC的解析式为y=x-2,根据三角形面积公式可判断PD∥BC,于是可设直线PD的解析式为y=x+p,然后把D点坐标代入求出p得到直线PD的解析式为y=x-$\frac{11}{4}$,最后把P(t,0)代入可求出t的值.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{1-b+c=0}\\{c=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-1}\\{c=-2}\end{array}\right.$,
所以抛物线解析式为y=x2-x-2;
抛物线的对称轴为直线x=$\frac{1}{2}$;
(2)y=x2-x-2=(x-$\frac{1}{2}$)2-$\frac{9}{4}$,
则D($\frac{1}{2}$,-$\frac{9}{4}$),
当y=0时,x2-x-2=0,解得x1=2,x2=-1,则B(2,0),
设直线BC的解析式为y=mx+n,
把B(2,0),C(0,-2)代入得$\left\{\begin{array}{l}{2m+n=0}\\{n=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=1}\\{n=-2}\end{array}\right.$,
∴直线BC的解析式为y=x-2,
∵△BDP和△CDP的面积相等,
∴PD∥BC,
设直线PD的解析式为y=x+p,
把D($\frac{1}{2}$,-$\frac{9}{4}$)代入得$\frac{1}{2}$+p=-$\frac{9}{4}$,解得p=-$\frac{11}{4}$,
∴直线PD的解析式为y=x-$\frac{11}{4}$,
把P(t,0)代入得t-$\frac{11}{4}$=0,解得t=$\frac{11}{4}$.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),通过解方程ax2+bx+c=0可得到抛物线与x轴的交点的横坐标.

 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论: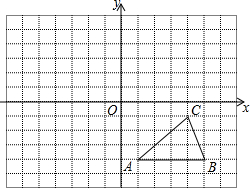 如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系,△ABC的顶点均在格点上.(不写作法)
如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系,△ABC的顶点均在格点上.(不写作法) 如图,点A的坐标为(8,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF、等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度为4.
如图,点A的坐标为(8,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF、等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度为4.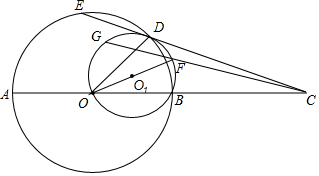 已知:AB是⊙O的直径,C为AB延长线上的一点,过点C作⊙O的割线,与⊙O交于D、E两点,OF是△BOD的外接圆O1的直径,连接CF并延长交⊙O1于点G.求证:O、A、E、G四点共圆.
已知:AB是⊙O的直径,C为AB延长线上的一点,过点C作⊙O的割线,与⊙O交于D、E两点,OF是△BOD的外接圆O1的直径,连接CF并延长交⊙O1于点G.求证:O、A、E、G四点共圆.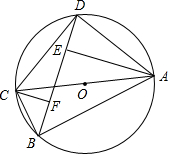 如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.
如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.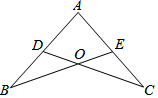 已知(如图):点D,E分别在AB,AC上,BE,CD交于O,且AB=AC,∠B=∠C.
已知(如图):点D,E分别在AB,AC上,BE,CD交于O,且AB=AC,∠B=∠C.