题目内容
7.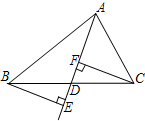 如图,已知BE⊥AD,CF⊥AD,BE=CF,由这三个条件组合运用可以得到若干结论,请你写出三个正确结论:△BDE≌△CDF,BD=CD,AD是△ABC的中线.
如图,已知BE⊥AD,CF⊥AD,BE=CF,由这三个条件组合运用可以得到若干结论,请你写出三个正确结论:△BDE≌△CDF,BD=CD,AD是△ABC的中线.
分析 根据已知条件得到△BDE≌△CDF,根据全等三角形的性质得到BD=CD.AD是△ABC的中线
解答 解:∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
在△BDE和△CDF中,
$\left\{\begin{array}{l}{∠BED=∠CFD}\\{∠BDE=∠CDF}\\{BE=CF}\end{array}\right.$
∴△BDE≌△CDF(AAS),
∴BD=CD.
∴AD是△ABC的中线.
故答案为:△BDE≌△CDF,BD=CD,AD是△ABC的中线.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.做题时要根据实际情况灵活运用.

练习册系列答案
相关题目
17.下列四个图案中,具有一个共有的性质,

那么下面四个数中,满足上述性质的一个是( )

那么下面四个数中,满足上述性质的一个是( )
| A. | 222 | B. | 707 | C. | 803 | D. | 609 |
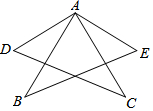 如图,AB=AC,AD=AE,CD=BE.请问∠DAB与∠EAC相等吗?请说明理由.
如图,AB=AC,AD=AE,CD=BE.请问∠DAB与∠EAC相等吗?请说明理由. 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论: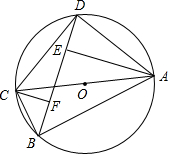 如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.
如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.