题目内容
8.如图,数轴上有A、B、C、D四个点,分别对应的数为a、b、c、d,且满足a,b是方程|x+9|=1的两根(a<b),(c-16)2与|d-20|互为相反数.
(1)求a、b、c、d的值;
(2)若A点以6个单位长度/秒的速度向右匀速运动,同时C点以2个单位长度/秒向左匀速运动,设运动时间为t秒,问t为多少时,A、C两点相距4个单位长度?
分析 (1)根据非负数的性质,及相反数的定义,可得出a、b、c、d的值;
(2)分两种情况讨论:在点A、C相遇之前,在点A、C相遇之后,分别列出方程求解即可.
解答 解:(1)∵a,b是方程|x+9|=1的两根(a<b),
解得:a=-10,b=-8,
∵(c-16)2与|d-20|互为相反数,
∵(c-16)2≥0,|d-20|≥0,
∴c-16=0,d-20=0,
可得:c=16,d=20;
(2)AC=16-(-10)=16,
在点A、C相遇之前:
由6t+4+2t=16,可得
t=1.5;
在点A、C相遇之后:
由6t-4+2t=16,可得
t=2.5;
综上所述,t为1.5或2.5秒时,A、C两点相距4个单位长度.
点评 本题考查了一元一次方程的应用,涉及了动点问题的计算,解答本题关键是掌握非负数的性质,注意分类讨论思想的运用.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
16. 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=$\frac{1}{2}$GE;
②△AGE≌△ECF;
③∠FCD=45°
其中,正确的结论有( )
 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=$\frac{1}{2}$GE;
②△AGE≌△ECF;
③∠FCD=45°
其中,正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.如果点A(m-2,2m)在第一、三象限的角平分线上,那么点N(-m+2,m-1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
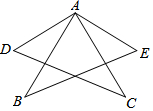 如图,AB=AC,AD=AE,CD=BE.请问∠DAB与∠EAC相等吗?请说明理由.
如图,AB=AC,AD=AE,CD=BE.请问∠DAB与∠EAC相等吗?请说明理由.
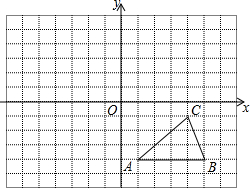 如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系,△ABC的顶点均在格点上.(不写作法)
如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系,△ABC的顶点均在格点上.(不写作法) 如图,点A的坐标为(8,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF、等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度为4.
如图,点A的坐标为(8,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF、等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度为4.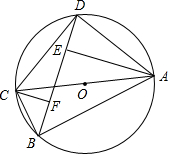 如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.
如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.