题目内容
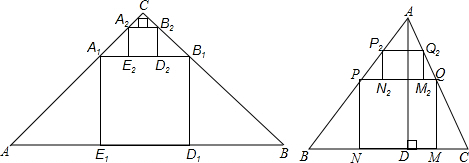
15.如图,(1)△ABC是斜边AB的长为3的等腰直角三角形,在△ABC内作第1个内接正方形A1B1D1E1(D1、E1在AB上,A1、B1分别在AC、BC上),再在△A1B1C内用同样的方法作第2个内接正方形A2B2D2E2,…如此下去,操作n次,则第一个内接正方形的边长是1,第n个小正方形AnBnDnEn 的边长是$\frac{1}{{3}^{(n-1)}}$.
(2)在△ABC中,BC=12,高AD=8,四边形PQMN为△ABC的内接矩形,(P在AB上,Q在AC上,M、N在BC上),
①求当PQ为何值时,矩形PQMN面积最大.
②若再在△APQ中作一个内接矩形P2Q2M2N2,如此下去,操作n次,求PnQn的长.(直接写出结果)
(3)解完上述两题,根据其中一题你还能归纳出怎样的数学结论,请简单的写出一条.
分析 (1)求出第一个、第二个、第三个内接正方形的边长,总结规律可得出第n个小正方形AnBnDnEn 的边长.
(2)设PQ=x,矩形PQMN面积为y,则根据△APQ∽△ABC的性质得到PN的长度,然后由矩形的面积公式列出y关于x的二次函数关系,所以根据二次函数最值的求法进行解答;
②利用(1)的解题过程写出规律;
(3)根据(1)、(2)总结出规律即可.
解答  解:(1)∵∠A=∠B=45°,
解:(1)∵∠A=∠B=45°,
∴AE1=A1E=A1B1=B1D1=D1B,
∴第一个内接正方形的边长=$\frac{1}{3}$AB=1.
同理可得:
第二个内接正方形的边长=$\frac{1}{3}$A1B1=$\frac{1}{9}$AB=$\frac{1}{3}$,
第三个内接正方形的边长=$\frac{1}{3}$A2B2=$\frac{1}{27}$AB=$\frac{1}{9}$,
…
故可推出第n个小正方形AnBnDnEn 的边长=$\frac{1}{{3}^{n}}$AB=$\frac{1}{{3}^{(n-1)}}$.
故答案为:1;$\frac{1}{{3}^{(n-1)}}$.
(2)①设PQ=x,矩形PQMN面积为y,AD交PQ于点E,
∵PQ∥BC,
∴△APQ∽△ABC,
∴$\frac{AE}{AD}$=$\frac{PQ}{AB}$,即$\frac{8-PN}{8}$=$\frac{x}{12}$,
∴PN=8-$\frac{2}{3}$x.
则y=PQ•PN=x•(8-$\frac{2}{3}$x)=-$\frac{2}{3}$(x-6)2+24.
∵-$\frac{2}{3}$<0,
∴该抛物线的开口方向向下,
故当PQ=6时,矩形PQMN面积最大;
②由①知,PQ=$\frac{12}{2}$,
同理:P1Q1=$\frac{12}{{2}^{2}}$,
P2Q2=$\frac{12}{{2}^{3}}$,
…
PnQn=$\frac{12}{{2}^{n}}$.
(3)根据(1)的解题过程可以得到结论:第n个小正方形AnBnDnEn 的面积是 $\frac{1}{{3}^{2(n-1)}}$.
根据(2)的解题过程可以得到:再在△APQ中作一个内接矩形P2Q2M2N2,如此下去,操作n次,PnQn的长为$\frac{12}{{2}^{n}}$.
点评 本题考查了相似综合题.解题时涉及到了相似三角形的判定与性质、等腰直角三角形的性质,解答本题的关键是求出前几个内接正方形的边长,得出一般规律.

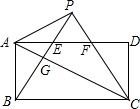 如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=3,将△ABC沿对角线AC折叠,点B恰好落在点P处,CP与AD交于点F,连接BP交AC于点G,交AD于点E,下列结论错误的是( )
如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=3,将△ABC沿对角线AC折叠,点B恰好落在点P处,CP与AD交于点F,连接BP交AC于点G,交AD于点E,下列结论错误的是( )| A. | AC=2AP | B. | △PBC是等边三角形 | ||
| C. | S△BGC=3S△AGP | D. | $\frac{PG}{CG}$=$\frac{1}{3}$ |
 (1)解方程组$\left\{\begin{array}{l}3x+4y=19\\ x-4y=1\end{array}\right.$
(1)解方程组$\left\{\begin{array}{l}3x+4y=19\\ x-4y=1\end{array}\right.$
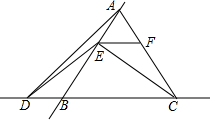 已知:△ABC是正三角形,且边长为1,点E是直线AB上的一个动点,过点E作BC的平行线交直线AC于点F,将线段EC绕点E旋转,使点C落在直线BC上的点D处;
已知:△ABC是正三角形,且边长为1,点E是直线AB上的一个动点,过点E作BC的平行线交直线AC于点F,将线段EC绕点E旋转,使点C落在直线BC上的点D处; 如图,等腰梯形ABCD,AB∥CD,AB=3$\sqrt{2}$,DC=$\sqrt{2}$,对角线AC⊥BD,平行于线段BD的直线MN、RQ分别以1个单位/秒、2个单位/秒的速度同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G,当直线RQ到达点C时两直线同时停止运动.记等腰梯形ABCD被直线MN扫过的面积为S1,被直线RQ扫过的面积为S2,若S2=mS1,则m的最小值是3.
如图,等腰梯形ABCD,AB∥CD,AB=3$\sqrt{2}$,DC=$\sqrt{2}$,对角线AC⊥BD,平行于线段BD的直线MN、RQ分别以1个单位/秒、2个单位/秒的速度同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G,当直线RQ到达点C时两直线同时停止运动.记等腰梯形ABCD被直线MN扫过的面积为S1,被直线RQ扫过的面积为S2,若S2=mS1,则m的最小值是3.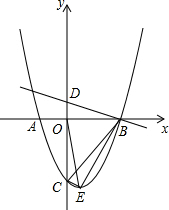 已知抛物线y=ax2-2x+c与x轴交于A(-1,0)、B两点,与y轴交于点C.对称轴为x=1,顶点为E,直线y=-$\frac{1}{3}$x+1交y轴于点D.
已知抛物线y=ax2-2x+c与x轴交于A(-1,0)、B两点,与y轴交于点C.对称轴为x=1,顶点为E,直线y=-$\frac{1}{3}$x+1交y轴于点D.