题目内容
7．
如图．已知AB∥EF，∠BAE的平分线交EF于点C，∠E=64°，则∠ACE的度数为（ ）| A． | 54° | B． | 58° | C． | 60° | D． | 64° |
分析 由AB∥EF，∠BAE的平分线交EF于点C，易证得△ACE是等腰三角形，然后由等边对等角，求得∠CAE=∠E=64°，继而求得答案．
解答 解：∵AB∥EF，
∴∠BAC=∠ACE，
∵AC平分∠BAE，
∴∠BAC=∠EAC，
∴∠EAC=∠ACE，
∴∠CAE=∠E=64°，
∴∠ACE=180°-∠E-∠CAE=58°．
故选B．
点评 此题考查了平行线的性质以及等腰三角形的性质，注意证得△ACE是等腰三角形是解此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．下列四个数中，与$\sqrt{11}$-2的值最接近的数是（ ）
| A． | $\frac{1}{2}$ | B． | 0 | C． | $\frac{3}{2}$ | D． | 2 |
如图，正六边形ABCDEF能由△ABO平移得到的图形有哪几个？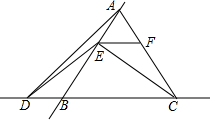
已知：△ABC是正三角形，且边长为1，点E是直线AB上的一个动点，过点E作BC的平行线交直线AC于点F，将线段EC绕点E旋转，使点C落在直线BC上的点D处；