题目内容
8.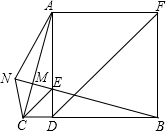 如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论:
如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论:①AC⊥BN;②△NCE为等边三角形;③BF=2AM;④BE+$\sqrt{2}$DE=DF,
其中正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 判断①:由根据正方形的性质得到AD=DB,∠3=45°,再CE∥DF得到∠2=∠3=45°,则CD=ED,接着证明△DBE≌△DAC得到∠1=∠5,然后根据三角形内角和定理易得∠AME=∠BDE=90°,所以AC⊥BN;
判断②:由∠AEB=105°可得到∠1=15°,∠NED=105°,则∠5=15°,∠NEC=60°,根据三角形外角性质得∠6=∠5+∠ACE=45°,所以∠MCE=30°,根据含30度的直角三角形三边的关系得到CE=2ME,由于CE=2MN,则ME=MN,根据线段中垂线的性质得CN=CE,于是可判断△NCE为等边三角形;
判断③:连结AB,如图,根据正方形的性质得∠ADB=45°,AB=$\sqrt{2}$BF,则∠ABM=30°,在Rt△ABM中,根据含30度的直角三角形三边的关系得到AB=2AM,所以$\sqrt{2}$BF=2AM,于是得到BF=$\sqrt{2}$AM;
判断④:先由AM垂直平分NE得到AN=AE,则∠ANE=∠AEN=75°,再根据三角形内角和计算出∠BAN=75°,于是得到BA=BN,则BN=DF,接着由CE=$\sqrt{2}$DE得到NE=$\sqrt{2}$DE,所以BN=BE+NE=BE+$\sqrt{2}$DE,则有DF=BE+$\sqrt{2}$DE.
解答 解:∵四边形ABCD为正方形,
∴AD=DB,∠3=45°,
∵CE∥DF,
∴∠2=∠3=45°,
∴△CDE为等腰直角三角形,
∴CD=ED,
在△DBE和△DAC中
$\left\{\begin{array}{l}{DB=DA}\\{∠BDE=∠ADC}\\{DE=DC}\end{array}\right.$,
∴△DBE≌△DAC,
∴∠1=∠5,
而∠DEB=∠AEM,
∴∠AME=∠BDE=90°,
∴AC⊥BN,所以①正确;
∵∠AEB=105°,
∴∠1=15°,∠NED=105°,
∴∠5=15°,∠NEC=105°-45°=60°,
而∠6=∠5+∠ACE=45°,
∴∠MCE=30°,
而CM⊥ME,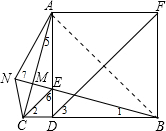
∴CE=2ME,
∵CE=2MN,
∴ME=MN,
∴CN=CE,
∴△NCE为等边三角形,所以②正确;
连结AB,如图,则∠ADB=45°,
而∠1=15°,
∴∠ABM=30°,
在Rt△ABM中,AB=2AM,
∵AB=$\sqrt{2}$BF,
∴$\sqrt{2}$BF=2AM,
∴BF=$\sqrt{2}$AM,所以③错误;
∵AM垂直平分NE,
∴AN=AE,
∴∠ANE=∠AEN=180°-∠AEB=75°,
而∠ABN=30°,
∴∠BAN=75°,
∴BA=BN,
而BA=DF,
∴BN=DF,
∵△CNE为等边三角形,
∴CE=NE,
而CE=$\sqrt{2}$DE,
∴NE=$\sqrt{2}$DE,
∴BN=BE+NE=BE+$\sqrt{2}$DE,
∴DF=BE+$\sqrt{2}$DE,所以④正确.
故选B.
点评 本题考查了四边形的综合题:熟练掌握正方形的性质、等边三角形的判定与性质和等腰直角三角形的判定与性质;会利用三角形全等证明角相等或利用等腰三角形的判定定理证明线段相等;记住含30度的直角三角形三边的关系.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案| A. | $\frac{1}{2}$ | B. | 0 | C. | $\frac{3}{2}$ | D. | 2 |
| A. | 70.5×105 | B. | 7.05×106 | C. | 705×104 | D. | 0.705×107 |
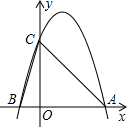 如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C. 如图,正六边形ABCDEF能由△ABO平移得到的图形有哪几个?
如图,正六边形ABCDEF能由△ABO平移得到的图形有哪几个?
 已知:△ABC是正三角形,且边长为1,点E是直线AB上的一个动点,过点E作BC的平行线交直线AC于点F,将线段EC绕点E旋转,使点C落在直线BC上的点D处;
已知:△ABC是正三角形,且边长为1,点E是直线AB上的一个动点,过点E作BC的平行线交直线AC于点F,将线段EC绕点E旋转,使点C落在直线BC上的点D处; 如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E,F,有下列结论:
如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E,F,有下列结论: