题目内容
20.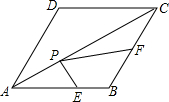 如图,在菱形ABCD中,AB=10,∠DAB=60°,P是对角线AC上一动点,E、F分别是线段AB和BC上的动点,则PE+PF的最小值是5$\sqrt{3}$.
如图,在菱形ABCD中,AB=10,∠DAB=60°,P是对角线AC上一动点,E、F分别是线段AB和BC上的动点,则PE+PF的最小值是5$\sqrt{3}$.
分析 当点E(E′)关于AC对称点E″与P、F(F′)三点共线且与AD垂直时,易求E″F(F′)的长就是PE+PF的最小值.
解答 解:如图所示,当点E(E′)关于AC对称点E″与P、F(F′)三点共线且与AD垂直时,PE+PF有最小值.
易证四边形BME″F′为矩形,
则BM=E″F′,
在Rt△ABM中,AB=2,∠BAD=60°,
∴E″F=BM=AB•sin∠BAD=5$\sqrt{3}$.
故答案是:5$\sqrt{3}$.
点评 本题考查了菱形的性质和轴对称-最短路线问题,解题的关键是得到PE+PF的最小值为菱形ABCD中AD边的高.

练习册系列答案
相关题目
7.下列说法错误的是( )
| A. | “伊利”纯牛奶消费者服务热线是4008169999,该十个数的中位数为7 | |
| B. | 服装店老板最关心的是卖出服装的众数 | |
| C. | 要了解全市初三近4万名学生2015年中考数学成绩情况,适宜采用全面调查 | |
| D. | 条形统计图能够显示每组中的具体数据,易于比较数据之间的差别 |
11.数学老师对黄华的8次单元考试成绩进行统计分析,要判断黄华的数学成绩是否稳定,老师需要知道黄华这8次数学成绩的( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
12.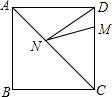 如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
 如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )| A. | 6 | B. | 8 | C. | 12 | D. | 10 |
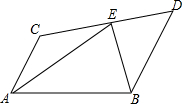 如图,已知梯形ABCD,AC∥BD,点E在CD上,有下列五个条件:
如图,已知梯形ABCD,AC∥BD,点E在CD上,有下列五个条件: