题目内容
7. 在一条公路上顺次有A、B、C三地,甲、乙两车同时从A地出发,分别匀速前往B地、C地,甲车到达B地停留一段时间后原速原路返回,乙车到达C地后立即原速原路返回,乙车比甲车早1小时返回A地,甲、乙两车各自行驶的路程y(千米)与时间x(时)(从两车出发时开始计时)之间的函数图象如图所示.
在一条公路上顺次有A、B、C三地,甲、乙两车同时从A地出发,分别匀速前往B地、C地,甲车到达B地停留一段时间后原速原路返回,乙车到达C地后立即原速原路返回,乙车比甲车早1小时返回A地,甲、乙两车各自行驶的路程y(千米)与时间x(时)(从两车出发时开始计时)之间的函数图象如图所示.(1)甲车到达B地停留的时长为3小时.
(2)求甲车返回A地途中y与x之间的函数关系式.
(3)直接写出两车在途中相遇时x的值.
分析 (1)根据题意和函数图象中的数据可以求得甲车到达B地停留的时长;
(2)根据题意和函数图象中的数据可以求得甲车返回A地途中y与x之间的函数关系式;
(3)根据题意可以求得两车在途中相遇时x的值.
解答 解:(1)由题意可得,
甲车到达B地停留的时长为:7-2-2=3(小时),
故答案为:3;
(2)设甲车返回A地途中y与x之间的函数关系式是y=kx+b,
$\left\{\begin{array}{l}{5k+b=160}\\{7k+b=320}\end{array}\right.$,得$\left\{\begin{array}{l}{k=80}\\{b=-240}\end{array}\right.$,
即甲车返回A地途中y与x之间的函数关系式是y=80x-240;
(3)由题意可得,
甲车的速度为:160÷2=80千米/时,
乙车的速度为:360÷(7-1)=60千米/时,
第一次相遇的时间为:160÷60=$\frac{8}{3}$h,
设第二次相遇的时间为xh,则(360-60x)=160或(360-60x)=320-(80x-240),
解得,x=$\frac{10}{3}$或x=10(舍去),
答:两车在途中相遇时x的值是$\frac{8}{3}$或$\frac{10}{3}$.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质解答.

练习册系列答案
相关题目

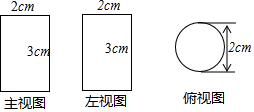 如图为一个几何体的三视图,
如图为一个几何体的三视图,
 如图,把“QQ”笑脸放在平面直角坐标系中,已知眼睛A、B的坐标分别为(-2,3),(0,3),则嘴C的坐标是(-1,1).
如图,把“QQ”笑脸放在平面直角坐标系中,已知眼睛A、B的坐标分别为(-2,3),(0,3),则嘴C的坐标是(-1,1). 如图,已知BD是矩形ABCD的对角线.
如图,已知BD是矩形ABCD的对角线.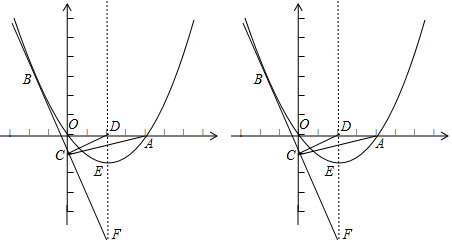
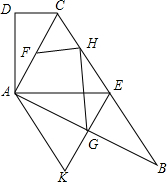 如图,在四边形ABCD中,AC平分∠BCD,AC2=CD•BC,E是BC的中点,AC⊥AB.
如图,在四边形ABCD中,AC平分∠BCD,AC2=CD•BC,E是BC的中点,AC⊥AB.