��Ŀ����
11��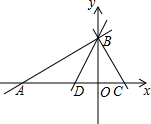 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=$\frac{1}{2}$x+6��x���ཻ�ڵ�A����y���ཻ�ڵ�B������B��ֱ��BC��AB��x���ڵ�C����OA��OC�ij��ֱ��Ƿ���x2+bx+c=0��������
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=$\frac{1}{2}$x+6��x���ཻ�ڵ�A����y���ཻ�ڵ�B������B��ֱ��BC��AB��x���ڵ�C����OA��OC�ij��ֱ��Ƿ���x2+bx+c=0����������1����b��c��ֵ
��2������B����һ��ֱ�߽�x���ڵ�D��ʹBDƽ�֡�ABC����ֱ��BD�Ľ���ʽ��
��3����ֱ��BD���Ƿ����һ��M������M��MN��BC��y���ڵ�N��ʹ��M��N��B��CΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
���� ��1�������Ա����뺯���Ķ�Ӧ��ϵ���ɵ�A��B�����꣬���ݻ��ഹֱ����ֱ����һ����ϵ���ij˻�Ϊ-1���ɵ�BC�Ľ���ʽ�����ݺ���ֵΪ�㣬�ɵ�C�����꣬���ݸ���ϵ���Ĺ�ϵ���ɵô𰸣�
��2�����ݽ�ƽ���߷ֶԱ����õ��߶��������ε��������߳ɱ������ɵ�D�����꣬���ݴ���ϵ�������ɵô𰸣�
��3���������ۣ���M1N1CB��ƽ���ı��Σ�����ƽ���ߵ�һ����ϵ����ȣ��ɵ�CN�Ľ���ʽ��MN�Ľ���ʽ������M�����������MN�Ľ���ʽ���ɵ�M������ꣻ�ڵ�M2N2BC��ƽ���ı��Σ�����MB��y�ᣬ�ɵ�M��ĺ����꣬��M��ĺ��������BD�Ľ���ʽ���ɵô𰸣�
��� �⣺��1����y=0ʱ��$\frac{1}{2}$x+6=0�����x=-12����A��-12��0����
��x=0ʱ��y=6����B��0��6����
����B��ֱ��BC��AB��x���ڵ�C����
BC�Ľ���ʽΪy=-2x+6��
��y=0ʱ��-2x+6=0�����x=3����C��3��0����
OA�ij�Ϊ12��OB�ij�Ϊ3��
OA��OC�ij��ֱ��Ƿ���x2+bx+c=0������������
-b=12+3��b=-15��c=12��3=36��
b=-15��c=36��
��2����D��a��0�������߶εĺͲ��
AD=��a+12����BD=��3-a����
�ɹ��ɶ�������
AB=$\sqrt{��-12��^{2}+{6}^{2}}$=6$\sqrt{5}$��BC=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$��
��BDƽ�֡�ABC����
$\frac{AD}{BD}$=$\frac{AC}{BC}$����$\frac{a+12}{3-a}$=$\frac{6\sqrt{5}}{3\sqrt{5}}$=2��
���a=2����D��-2��0����
��BD�Ľ���ʽΪy=kx+b��
��B��D������������ʽ����
$\left\{\begin{array}{l}{b=6}\\{-2k+b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=3}\\{b=6}\end{array}\right.$��
BD�Ľ���ʽΪy=3x+6��
��3����M��a��3a+6������ͼ1��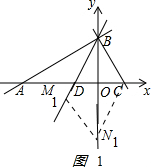
�ٵ�M1N1CB��ƽ���ı���ʱ��N1C��BD��M1N1��BC����CN1�Ľ���ʽΪy=3x+b��
��C��3��0�����뺯������ʽ����3��3+b=0�����b=-9����N1��0��-9����
M1N1�Ľ���ʽΪy=-2x-9����M��a��3a+6�����뺯������ʽ����
-2a-9=3a+6��
���a=-3��3a+6=-3����M1��-3��-3����
��ͼ2��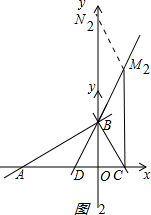
�ڵ�M2N2BC��ƽ���ı���ʱ��M2C��y�ᣬ
M2�ĺ�������C��ĺ�������ȣ�
��x=3����BD�Ľ���ʽ����y=3��3+6=15��
��M2��3��15����
������������ֱ��BD�ϴ���һ��M������M��MN��BC��y���ڵ�N��ʹ��M��N��B��CΪ������ı�����ƽ���ı��Σ�M1��-3��-3����M2��3��15����
���� ���⿼����һ�κ����ۺ��⣬�����˺������Ա����Ķ�Ӧ��ϵ���ó�A��B��C�����꣬�����˸���ϵ���Ĺ�ϵ����ƽ���ߵ����ʣ�ƽ���ߵ����ʣ�ƽ���ߵ�һ�����ϵ����ȣ�����֪ʶ��϶࣬�ۺ��Խ�ǿ����Ŀ��һ���Ѷȣ�

 �Ľ���ǣ�������
�Ľ���ǣ�������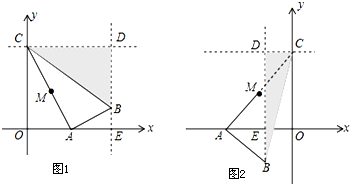
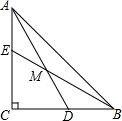 ��ͼ����ABC�У�AC=BC����ACB=90�㣬D��E�ֱ���BC��AC��һ�㣬BD=AE��BE��AD����M��
��ͼ����ABC�У�AC=BC����ACB=90�㣬D��E�ֱ���BC��AC��һ�㣬BD=AE��BE��AD����M��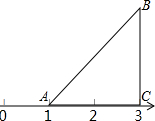 ��ͼ������ֱ��������ABC��ֱ�DZ�AC���������ϣ���A��ʾ������1����C��ʾ������3����AΪ��ת������ʱ����ת��ABC��
��ͼ������ֱ��������ABC��ֱ�DZ�AC���������ϣ���A��ʾ������1����C��ʾ������3����AΪ��ת������ʱ����ת��ABC��


