题目内容
6.如图1和图2,在平面直角坐标系中,点C的坐标为(0,4),A是x轴上的一个动点,M是线段AC的中点.把线段AM以A为旋转中心、按顺时针方向旋转90°得到AB.过B作x轴的垂线、过点C作y轴的垂线,两直线交于点D,直线DB交x轴于点E.设A点的横坐标为m.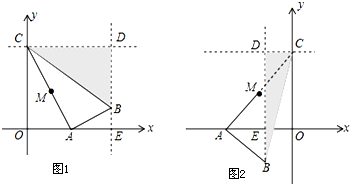
(1)若m=3,则点B的坐标为(5,1.5);若m=-3,则点B的坐标为(-1,-1.5);
(2)若m>0,△BCD的面积为S,则m为何值时,S=6?
(3)是否存在m,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时t的值;若不存在,请说明理由.
分析 (1)首先由勾股定理求得线段AC的长,然后利用△AOC∽△BOA求得线段BE、AE的长,从而求得点B的坐标;
(2)分0<m<8时和m>8时,利用△AOC∽△BEA,根据相似比表示出点B的坐标后,利用面积为6求得t值即可;
(3)分0<m<8、m>8、-2<m<0、m<-2,根据△AOC∽△CDB和△AOC∽△BDC两种情况得到比例式即可求得t值.
解答 解:(1)∵C的坐标为(0,4),m=3或-3,
∴由勾股定理得:AC=5,
∵△AOC∽△BEA且相似比为$\frac{AC}{AB}$=2,AO=3 OC=4
∴AE=2,BE=1.5
∴点B的坐标为(5,1.5)或(-1,-1.5 ),
故答案为:(5,1.5),(-1,-1.5 ); 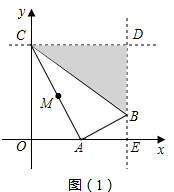 (2)①当0<m<8时,如图(1)
(2)①当0<m<8时,如图(1)
△AOC∽△BEA且相似比为$\frac{AC}{AB}$,
求得点B的坐标为(m+2,$\frac{1}{2}$),
∴S=$\frac{1}{2}$DC•DB=$\frac{1}{2}$(m+2)×(4-$\frac{1}{2}$m)=6,
解得 m=2或4,
②当m>8时,如图(2)
S=$\frac{1}{2}$DC•DB=$\frac{1}{2}$(m+2)×($\frac{1}{2}$m-4)=6,
解得 m=10或m=-4(舍去)
∴m=2,m=4,m=10,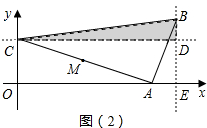
(3)①当0<m<8时,如图(1)
若△AOC∽△CDB
∴$\frac{AO}{CD}$=$\frac{CO}{BD}$即:$\frac{m}{m+2}$=$\frac{4}{4-\frac{1}{2}m}$
∴m无解,
若△AOC∽△BDC,同理,解得m=2$\sqrt{5}$-2或m=-2$\sqrt{5}$-2(不合题意舍去),
②当m>8时,如图(2)
若△AOC∽△CDB,
∴$\frac{AO}{CD}$=$\frac{CO}{BD}$即:$\frac{m}{m+2}$=$\frac{4}{\frac{1}{2}m-4}$,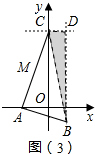
解得m=±4$\sqrt{5}$+8,取m=4$\sqrt{5}$+8,
若△AOC∽△BDC,同理,解得m无解,
③当-2<m<0时,如图(3),
若△AOC∽△CDB,
∴$\frac{AO}{CD}=\frac{CO}{BD}$即:$\frac{-m}{m+2}$=$\frac{4}{4-\frac{1}{2}m}$,
解得m=4$\sqrt{5}$+8(不合题意舍去)或m=-4$\sqrt{5}$+8,
若△AOC∽△BDC,同理,解得m无解,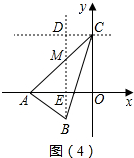
④当m<-2时,如图(4)
若△AOC∽△CDB,
∴$\frac{AO}{CD}=\frac{CO}{BD}$,即:$\frac{-m}{-m-2}$=$\frac{4}{4-\frac{1}{2}m}$,
则m无解,
若△AOC∽△BDC,同理,解得m=-2$\sqrt{5}$-2(不合题意舍去)或m=-2$\sqrt{5}$+2(不合题意舍去);
则m=2$\sqrt{5}$-2,m=4$\sqrt{5}$+8,m=-4$\sqrt{5}$+8.
点评 本题考查了相似形的综合题,比较繁琐,难度很大,解答此题的关键是画出图形作出辅助线,结合相似三角形的性质利用比例式列出方程解答.体现了数形结合在解题中的重要作用.

 全优点练单元计划系列答案
全优点练单元计划系列答案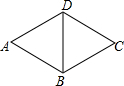 如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )
如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )| A. | 一个 | B. | 两个 | C. | 三个 | D. | 四个 |
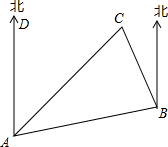 如图是A、B、C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.
如图是A、B、C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.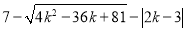 的结果是( )
的结果是( )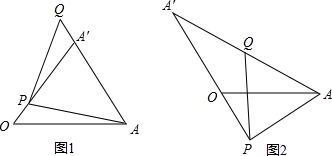
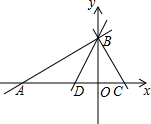 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+6与x轴相交于点A,与y轴相交于点B,过点B作直线BC⊥AB交x轴于点C,且OA和OC的长分别是方程x2+bx+c=0的两个根
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+6与x轴相交于点A,与y轴相交于点B,过点B作直线BC⊥AB交x轴于点C,且OA和OC的长分别是方程x2+bx+c=0的两个根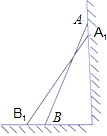 小明和同桌小聪在课后复习时,对课本“目标与评定”中一道思考题,进行了认真的探索
小明和同桌小聪在课后复习时,对课本“目标与评定”中一道思考题,进行了认真的探索