题目内容
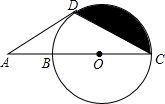 如图,B、O是线段AC的三等分点,以O为圆心,OC为半径作⊙O,D为⊙为上一点且DC=DA.
如图,B、O是线段AC的三等分点,以O为圆心,OC为半径作⊙O,D为⊙为上一点且DC=DA.(1)判断AD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为2,求阴影部分的面积.
考点:切线的判定,扇形面积的计算
专题:
分析:(1)连接OD、BD,根据OD=OC,DA=DC,求得∠A=∠C=∠ODC,根据已知求得AO=BC,进而根据SAS证得△AOD≌△CBD,从而求得∠ADO=∠CDB=90°,即可证得AD是⊙O的切线.
(2)先求得∠COD=120°,进而根据S阴影=S扇形-S△COD即可求得阴影部分的面积.
(2)先求得∠COD=120°,进而根据S阴影=S扇形-S△COD即可求得阴影部分的面积.
解答: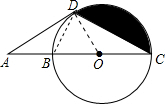 解:(1)AD是⊙O的切线,证明如下:
解:(1)AD是⊙O的切线,证明如下:
连接OD、BD,
∵OD=OC,DA=DC,
∴∠A=∠C=∠ODC
∵B、O是线段AC的三等分点,
∴AB=BO=CO,
即AO=BC,
在△AOD和△CBD中,
,
∴△AOD≌△CBD(SAS),
∴∠ADO=∠CDB,BD=OD,
∵BC是⊙O的直径,
∴∠ADO=∠CDB=90°,
∴OD⊥DA,
∴AD是⊙O的切线.
(2)∵BD=OD=OB,
∴△OBD是等边三角形,
∴∠COD=120°,
∵⊙O的半径为2,
∴S△COD=
,
∴S阴影=S扇形-S△COD=
-
=
π-
.
 解:(1)AD是⊙O的切线,证明如下:
解:(1)AD是⊙O的切线,证明如下:连接OD、BD,
∵OD=OC,DA=DC,
∴∠A=∠C=∠ODC
∵B、O是线段AC的三等分点,
∴AB=BO=CO,
即AO=BC,
在△AOD和△CBD中,
|
∴△AOD≌△CBD(SAS),
∴∠ADO=∠CDB,BD=OD,
∵BC是⊙O的直径,
∴∠ADO=∠CDB=90°,
∴OD⊥DA,
∴AD是⊙O的切线.
(2)∵BD=OD=OB,
∴△OBD是等边三角形,
∴∠COD=120°,
∵⊙O的半径为2,
∴S△COD=
| 3 |
∴S阴影=S扇形-S△COD=
| 120π×22 |
| 360 |
| 3 |
| 4 |
| 3 |
| 3 |
点评:本题考查了切线的判定,三角形全等的判定和性质,等边三角形的判定和性质,扇形面积的计算等,作出辅助线根据直角三角形是解题的关键.

练习册系列答案
相关题目
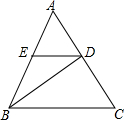 已知:如图,BD是等腰三角形ABC的底边AC上的高,∠ADE=∠C.求证:△BDE是等腰三角形.
已知:如图,BD是等腰三角形ABC的底边AC上的高,∠ADE=∠C.求证:△BDE是等腰三角形. 如图所示是淮河的一段,两岸AB∥CD,河岸AB上有一排大树.小明为了测量该段河的宽度,先用测角仪在河岸CD的M处测得∠α=33°,然后沿河岸走40米到达N点,测得∠β=64°.请你帮小明算出河宽ER(结果保留整数).
如图所示是淮河的一段,两岸AB∥CD,河岸AB上有一排大树.小明为了测量该段河的宽度,先用测角仪在河岸CD的M处测得∠α=33°,然后沿河岸走40米到达N点,测得∠β=64°.请你帮小明算出河宽ER(结果保留整数).
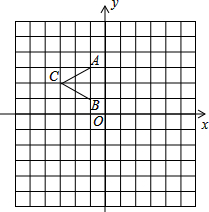 如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)
如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)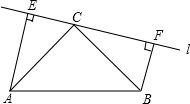 如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足为E,F.
如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足为E,F.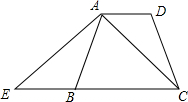 如图,在四边形ABCD中,AD∥BC,且AB=CD,∠D=∠BAD,延长线段CB到E,使BE=AD,连接AE、AC
如图,在四边形ABCD中,AD∥BC,且AB=CD,∠D=∠BAD,延长线段CB到E,使BE=AD,连接AE、AC 在Rt△ABC中,∠C=90°,BC=2
在Rt△ABC中,∠C=90°,BC=2