题目内容
 如图所示是淮河的一段,两岸AB∥CD,河岸AB上有一排大树.小明为了测量该段河的宽度,先用测角仪在河岸CD的M处测得∠α=33°,然后沿河岸走40米到达N点,测得∠β=64°.请你帮小明算出河宽ER(结果保留整数).
如图所示是淮河的一段,两岸AB∥CD,河岸AB上有一排大树.小明为了测量该段河的宽度,先用测角仪在河岸CD的M处测得∠α=33°,然后沿河岸走40米到达N点,测得∠β=64°.请你帮小明算出河宽ER(结果保留整数).(参考数据:sin33°≈0.55,cos33°≈0.84,tan33°≈0.65,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
考点:解直角三角形的应用
专题:
分析:过点E作CD垂线,垂足为R,在Rt△NRE中,NR=
米,在Rt△MRE中,MR=
米,列出等式
-
=40,即可求出ER的长.
| ER |
| tanβ |
| ER |
| tanα |
| ER |
| tanα |
| ER |
| tanβ |
解答: 解:如图,过点E作CD垂线,垂足为R,
解:如图,过点E作CD垂线,垂足为R,
在Rt△NRE中,NR=
米,
在Rt△MRE中,MR=
米,
∴
-
=40,
即
-
=40,
解得ER≈38米.
 解:如图,过点E作CD垂线,垂足为R,
解:如图,过点E作CD垂线,垂足为R,在Rt△NRE中,NR=
| ER |
| tanβ |
在Rt△MRE中,MR=
| ER |
| tanα |
∴
| ER |
| tanα |
| ER |
| tanβ |
即
| ER |
| tan33° |
| ER |
| tan64° |
解得ER≈38米.
点评:本题考查了解直角三角形的应用,熟悉三角函数的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将数据36000000用科学记数法表示是( )
| A、3.6×107 |
| B、0.36×108 |
| C、36×107 |
| D、3.6×106 |
2013年12月14日20时59分,7500牛变推力发动机开机,嫦娥三号开始动力下降,嫦娥三号以1.7千米/秒的速度向月球降落,随后降落相机开机,经过主减速段,嫦娥三号的速度降到只有约600米/秒,请将7500牛精确到千位可表示为( )
| A、7000牛 |
| B、7.5×103牛 |
| C、8×103牛 |
| D、75×102牛 |
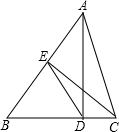 如图,在△ABC中,AD⊥BC,CE⊥AB,D,E为垂足,联结DE.
如图,在△ABC中,AD⊥BC,CE⊥AB,D,E为垂足,联结DE. 每个小正方形边长均为1,求四边形ABCD的边长和面积.
每个小正方形边长均为1,求四边形ABCD的边长和面积.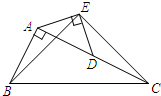 如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试判断△BCE的形状,并证明你的结论.
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试判断△BCE的形状,并证明你的结论.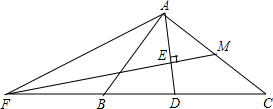 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF交CB的延长线于点F,交AD于点E,交AC于点M.
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF交CB的延长线于点F,交AD于点E,交AC于点M.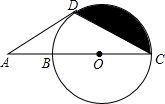 如图,B、O是线段AC的三等分点,以O为圆心,OC为半径作⊙O,D为⊙为上一点且DC=DA.
如图,B、O是线段AC的三等分点,以O为圆心,OC为半径作⊙O,D为⊙为上一点且DC=DA.