题目内容
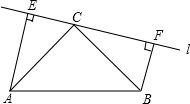 如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足为E,F.
如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足为E,F.(1)求证:△ACE≌△CBF;
(2)当直线l不与底边AB相交时,试探索EF、AE、BF三条线段的大小关系,并说明理由.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据垂直的定义可得∠AEC=∠CFB=90°,然后求出∠EAC=∠FCB,再利用“角角边”证明即可;
(2)根据全等三角形对应边相等可得EC=BF,AE=CF,再根据EF=EC+CF等量代换即可得解.
(2)根据全等三角形对应边相等可得EC=BF,AE=CF,再根据EF=EC+CF等量代换即可得解.
解答:(1)证明:∵AE⊥EF,BF⊥EF
∴∠AEC=∠CFB=90°,
∴∠EAC+∠ECA=90°,
∵∠ACB=90°,
∴∠FCB+∠ECA=90°,
∴∠EAC=∠FCB,
在△ACE和△CBF中,
,
∴△ACE≌△CBF(AAS);
(2)解:EF=AE+BF.
理由如下:∵△ACE≌△CBF,
∴EC=BF,AE=CF,
∴EF=EC+CF=AE+BF.
∴∠AEC=∠CFB=90°,
∴∠EAC+∠ECA=90°,
∵∠ACB=90°,
∴∠FCB+∠ECA=90°,
∴∠EAC=∠FCB,
在△ACE和△CBF中,
|
∴△ACE≌△CBF(AAS);
(2)解:EF=AE+BF.
理由如下:∵△ACE≌△CBF,
∴EC=BF,AE=CF,
∴EF=EC+CF=AE+BF.
点评:本题考查了全等三角形的判定与性质,同角的余角相等的性质,熟练掌握三角形全等的判断方法并找出全等的条件是解题的关键.

练习册系列答案
相关题目
 如图,等边△ABC中,高AD、BE相交于F点,则图中等腰三角形的个数(除△ABC外)是( )
如图,等边△ABC中,高AD、BE相交于F点,则图中等腰三角形的个数(除△ABC外)是( )| A、5 | B、6 | C、7 | D、8 |
 如图,二次函数y=ax2+bx的图象经过原点,顶点的纵坐标为2,若一元二次方程
如图,二次函数y=ax2+bx的图象经过原点,顶点的纵坐标为2,若一元二次方程ax2+bx+k=0有实数根,则k的取值范围是( )
| A、k≤-2 | B、k≥2 |
| C、k≤2 | D、k≥-2 |
2013年12月14日20时59分,7500牛变推力发动机开机,嫦娥三号开始动力下降,嫦娥三号以1.7千米/秒的速度向月球降落,随后降落相机开机,经过主减速段,嫦娥三号的速度降到只有约600米/秒,请将7500牛精确到千位可表示为( )
| A、7000牛 |
| B、7.5×103牛 |
| C、8×103牛 |
| D、75×102牛 |
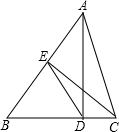 如图,在△ABC中,AD⊥BC,CE⊥AB,D,E为垂足,联结DE.
如图,在△ABC中,AD⊥BC,CE⊥AB,D,E为垂足,联结DE.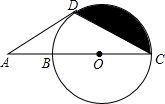 如图,B、O是线段AC的三等分点,以O为圆心,OC为半径作⊙O,D为⊙为上一点且DC=DA.
如图,B、O是线段AC的三等分点,以O为圆心,OC为半径作⊙O,D为⊙为上一点且DC=DA.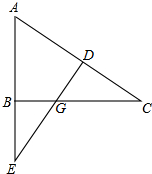 已知:如图,∠ABC=90°,DE⊥AC于点D,交BC于点G,交AB的延长线于点E,且AE=AC.求证:
已知:如图,∠ABC=90°,DE⊥AC于点D,交BC于点G,交AB的延长线于点E,且AE=AC.求证: 如图所示,抛物线y=-(x-1)2+4与x轴交于A、B两点,与y轴交于C点,顶点为D.若抛物线上有一点P(点P不与点C重合),使得S△DCB=S△PCB,则这样的点P总共存在
如图所示,抛物线y=-(x-1)2+4与x轴交于A、B两点,与y轴交于C点,顶点为D.若抛物线上有一点P(点P不与点C重合),使得S△DCB=S△PCB,则这样的点P总共存在