题目内容
14．已知平行四边形ABCD中，点A，B，C的坐标分别是A（-1，1），B（1，-2），C（4，2），则点D的坐标是（2，5）．分析 根据平行四边形的性质和A、B、C的坐标得出A点的纵坐标和B点的纵坐标的差为3，横坐标差为-2，即可得出点D的坐标．
解答 解：∵四边形ABCD是平行四边形，
∴CD∥AB，AD∥BC，
∵A（-1，1），B（1，-2），C（4，2），
∴A点的纵坐标和B点的纵坐标的差为3，横坐标差-2，
∴D（2，5），
故答案为：（2，5）．
点评 本题考查了平行四边形性质和坐标与图形性质；熟练掌握平行四边形的性质是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．下列命题中逆命题是真命题的是（ ）
| A． | 对顶角相等 | |
| B． | 若两个角都是45°，那么这两个角相等 | |
| C． | 全等三角形的对应角相等 | |
| D． | 两直线平行，同位角相等 |
5．下列根式中，与$\sqrt{20}$互为同类二次根式的是（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{5}$ | D． | $\sqrt{6}$ |
9．方程（x-2）2+4=0的解是（ ）
| A． | x1=x2=0 | B． | x1=2，x2=-2 | C． | x1=0，x2=4 | D． | 没有实数根 |
6．方程x-2=0的解是（ ）
| A． | $\sqrt{2}$ | B． | $-\sqrt{2}$ | C． | 2 | D． | -2 |
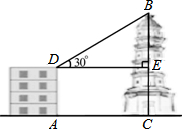如图，大楼AD和塔BC都垂直于地面AC，大楼AD高50米，和大楼AD相距90米的C处有一塔BC，某人在楼顶D处测得塔顶B的仰角∠BDE=30°，且∠BED=90°，求塔高BC．（结果保留整数，参考数据：$\sqrt{2}≈$1.41，$\sqrt{3}≈1.73$）