题目内容
20. 如图,?ABCD中,E为BC边上一点,且AB=AE.
如图,?ABCD中,E为BC边上一点,且AB=AE.(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
分析 (1)先证明∠B=∠EAD,然后利用SAS可进行全等的证明;
(2)证明△ABE为等边三角形,可得∠BAE=60°,求出∠BAC的度数,即可得∠AED的度数.
解答 (1)证明:∵在平行四边形ABCD中,AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,$\left\{\begin{array}{l}{AB=AE}&{\;}\\{∠ABC=∠EAD}&{\;}\\{BC=AD}&{\;}\end{array}\right.$,
∴△ABC≌△EAD(SAS).
(2)解:∵AE平分∠DAB,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB=∠B,
∴△ABE为等边三角形,
∴∠BAE=60°,
∴∠BAC=∠BAE+∠EAC=60°+25°=85°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=85°.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质,解答本题注意掌握平行四边形的对边平行且相等的性质.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
10.要调查昆明市民喜欢看的电视节目,应关注的是哪个数据的代表( )
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 加权平均数 |
11.下列四种正多边形中,用同一种图形不能铺满平面的是( )
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
15. 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )| A. | x>-2 | B. | x<-2 | C. | -3<x<-2 | D. | -3<x<-1 |
9.下列能够判定一个四边形是正方形的条件是( )
①一组邻边相等且对角线相等并互相平分;
②对角线互相垂直平分;
③四条边相等且四个内角也相等;
④对角线相等的菱形.
①一组邻边相等且对角线相等并互相平分;
②对角线互相垂直平分;
③四条边相等且四个内角也相等;
④对角线相等的菱形.
| A. | ①②④ | B. | ①③④ | C. | ③④ | D. | ①②③④ |
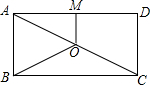 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=3,AD=4,则四边形ABOM的周长为9.
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=3,AD=4,则四边形ABOM的周长为9.