题目内容

8．若两个多边形的边数之比为3：4，两个多边形的内角总和为3060°，则这两个多边形的边数分别是9、12．

分析 设两个多边形的边数分别是3x和4x，利用两个多边形的内角和为3060°，即可列出方程，进而求解．

解答 解：设两个多边形的边数分别是3x、4x，
则（3x-2）•180+（4x-2）•180=3060，
解得x=3，
3x=9，
4x=12．
则两个多边形的边数分别是9、12．
故答案为：9、12．

点评 本题考查了多边形内角与外角，解答本题的关键在于熟练掌握多边形内角与外角和公式．

练习册系列答案
相关题目
2．如图，我县再创建园林卫生城市的过程中，某居民小区有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，计划将阴影部分进行绿化，中间将修建一个底座边长为（a+b）米雕塑，则绿化的面积是多少平方米？并求出当a=3，b=2时的绿化面积．
19．下列计算正确是（　　）
A．（x+2）（2-x）=x2-4B．（2x+y2）（2x-y2）=4x2-y4
C．（3x2+1）（3x2-1）=9x2-1D．（x+2）（x-3）=x2-6
16．在△ABC中，BC边上的高AD=4，若BC=4，则△ABC周长最小值是4$\sqrt{5}$+4．
3．已知6是a和b的比例中项，则$\sqrt{ab}$-$\frac{1}{\sqrt{ab}}$=$\frac{35}{6}$．
13．在平面直角坐标系中，以原点为圆心，1为半径的圆，与直线y=x-$\sqrt{2}$的位置关系是（　　）
A．相交B．相切C．相离D．以上都有可能
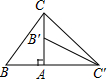20．如图，在直角三角形ABC中，∠BAC=90°，∠B=60°，AC=3，将三角形ABC绕点A按顺时针方向旋转90°，得到直角三角形AB'C'（点B'与点B是对应点，点C'与点C是对应点），连接CC'，则AC'=3，∠AC'B'=30°，∠AC'C=45°．
17．已知：关于x的方程：x2-2（k+1）x+k2+4=0
（1）当k取何值时，方程有两个实数根？
（2）若△ABC是等腰三角形，BC=4，AB、AC的长是这个方程的两个根，求△ABC的周长．
18．如图，在长方体ABCD-EFGH中，与棱AD所在的直线既不相交也不平行的棱共有（　　）
A．1条B．2条C．3条D．4条

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网