题目内容
17.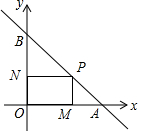 如图,P点的坐标为(3,2),过P点的直线AB分别交x轴和y轴的正半轴于A,B两点,作PM⊥x轴于M点,作PN⊥y轴于N点,若△PAM的面积与△PBN的面积的比为$\frac{4}{9}$,则直线AB的解析式为y=-x+5.
如图,P点的坐标为(3,2),过P点的直线AB分别交x轴和y轴的正半轴于A,B两点,作PM⊥x轴于M点,作PN⊥y轴于N点,若△PAM的面积与△PBN的面积的比为$\frac{4}{9}$,则直线AB的解析式为y=-x+5.
分析 求出△PMA∽△BNP,根据相似三角形的性质求出BN和AM长,求出A、B的坐标,设直线AB的解析式为y=kx+b,把A、B的坐标代入求出K、B值,即可得出答案.
解答 解:∵PM⊥x轴,PN⊥y中,x轴⊥y轴,
∴∠BNP=∠PMA=90°,PN∥x轴,
∴∠BPN=∠PAO,
∴△PMA∽△BNP,
∵△PAM的面积与△PBN的面积的比为$\frac{4}{9}$,
∴($\frac{AM}{PN}$)2=($\frac{PM}{BN}$)2=$\frac{4}{9}$,
∵P(3,2),
∴PN=3,PM=2,
∴AM=2,BN=3,
∴A(5,0),B(0,5),
设直线AB的解析式为y=kx+b,
把A、B的坐标代入得:$\left\{\begin{array}{l}{b=5}\\{5k+b=0}\end{array}\right.$,
解得:k=-1,b=5,
即直线AB的解析式为y=-x+5,
故答案为:y=-x+5.
点评 本题考查了一次函数的性质,用待定系数法求一次函数解析式,相似三角形的性质和判定等知识点,能求出A、B的坐标是解题的关键.

练习册系列答案
相关题目
8.已知一个三角形的两边长分别为3和4,则第三边的长不可能的是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.已知a+$\frac{1}{a}$=$\sqrt{6}$,则a-$\frac{1}{a}$的值为( )
| A. | $\sqrt{2}$ | B. | ±$\sqrt{2}$ | C. | 2 | D. | ±2 |
9.以下列各组数据为边不能组成直角三角形的一组数据是( )
| A. | 3,4,5 | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | 6,8,10 | D. | 5,12,13 |
12. 如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=50°,则∠CAD的大小为( )
如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=50°,则∠CAD的大小为( )
 如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=50°,则∠CAD的大小为( )
如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=50°,则∠CAD的大小为( )| A. | 50° | B. | 65° | C. | 80° | D. | 60° |
 如图,△ABC的三个顶点都在正方形网格的格点上,则sin∠ACB的值为$\frac{\sqrt{5}}{5}$.
如图,△ABC的三个顶点都在正方形网格的格点上,则sin∠ACB的值为$\frac{\sqrt{5}}{5}$. 如图,在?ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.
如图,在?ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.