题目内容
当k满足条件
时,关于x的一元二次方程kx2+(k-1)x+k2+3k=0是否存在实数根x=0?若存在求出k值,若不存在请说明理由.
|
考点:解一元一次不等式组,一元二次方程的解
专题:
分析:首先解不等式求得k的范围,然后把x=0代入方程求得k的值,根据解不等式组得到的k的范围进行判断.
解答:解:
,
解①得:k≤4,
解②得:k≥-7,
则不等式组的解集是:-7≤k≤4,
把x=0代入方程解得k=0或k=-3,
∵k=0不满足方程为一元二次方程,
∴k=-3.
|
解①得:k≤4,
解②得:k≥-7,
则不等式组的解集是:-7≤k≤4,
把x=0代入方程解得k=0或k=-3,
∵k=0不满足方程为一元二次方程,
∴k=-3.
点评:本题主要考查了一元一次不等式解集的求法,其简便求法就是用口诀求解,求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
相关题目
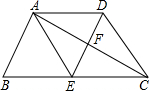 如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形.
如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形. 如图,在平面直角坐标系中,已知A点坐标(4,0),B点坐标(0,8),点M是线段OA上一动点(不与点O、点A重合),点N是线段OB上一动点,且运动时始终保持ON=2AM,连接MN,并作△OMN的角平分线OD交线段MN于点D.
如图,在平面直角坐标系中,已知A点坐标(4,0),B点坐标(0,8),点M是线段OA上一动点(不与点O、点A重合),点N是线段OB上一动点,且运动时始终保持ON=2AM,连接MN,并作△OMN的角平分线OD交线段MN于点D.